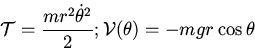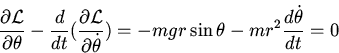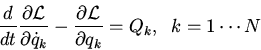![next]()
![up]()
![previous]()
Next: About
this document ...
8. Lagrangian
equations of motion
LAST TIME
- Introduced generalized coordinates, velocities and forces.
- Defined holonomic, scleronomic and rheonomic constraints.
- Showed how to determine number of degrees of freedom.
TODAY
we
will use these concepts and define the Lagrangian and derive the
Lagrangian equations of motion.
Let us assume that we are dealing
with a system which can be described by the Cartesian coordinates
in an inertial reference frame. The kinetic energy is
The equations of motion are given by Newton's second law
where 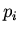 is the
is the 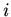 th component of
the momentum, and
th component of
the momentum, and 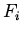 is the component of the force acting in the
direction of
is the component of the force acting in the
direction of 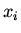 . These forces may include holonomic forces of
constraint. Let us assume that when these have been eliminated we have
. These forces may include holonomic forces of
constraint. Let us assume that when these have been eliminated we have 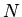 degrees of freedom described by generalized coordinates
degrees of freedom described by generalized coordinates
We now imagine that these equations have been substituted into the
expression for the kinetic energy
We have
Next
and we find
and
We use these result to write
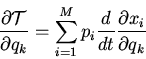 |
(1) |
and
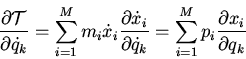 |
(2) |
Next take the time derivative of (2)
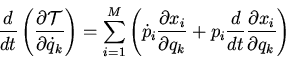 |
(3) |
For the first term inside the sum on the right hand side of(3) we use the
definition of generalized force from lecture 7
while for the second term we use (1) to find
We know assume that the generalized force can be split up into two
contributions
The first contribution is a conservative force derived from a
velocity independent potential. The second term represents "left-overs"
such as e.g. friction or drag forces.
We also define the
Lagrangian
Since we have assumed that the potential and the constraints are velocity
independent
we find Lagrangian equation of motion
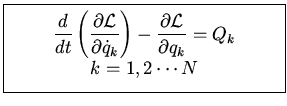
Note
that there is one equation for each degree of freedom. In the special case that
all forces are conservative and derived from a velocity independent potential
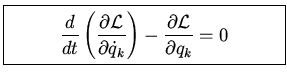
You
might think that we have only taken something relatively simple (Newton's
equations) and made it into something complicated (Lagrange's equations).
Actually, this is not the case: we will find that in most cases the Lagrangian
approach is the easiest to work with, when solving problems of even moderate
difficulty. Furthermore, we will find that the more complicated the problem the
greater the advantage of using the Lagrangian approach.
EXAMPLE
As
our first example consider the slider block problem of the last
lecture. The kinetic energy is in terms of the generalized coordinates 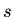 and
and 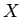 is
is
The potential energy is
We have
The equations of motion are thus
These equations of motion are the same as we found last time using
Newtonian mechanics. The main difference is that there is no need to bother
about the free body diagram or the normal forces 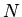 and
and 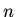 .
.
EXAMPLE
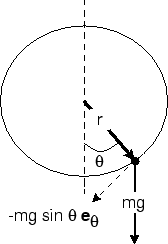
The pendulum
Instead of using the Cartesian coordinates of the mass it is convenient
describe the motion by the angle 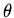 . The length of
the pendulum,
. The length of
the pendulum, 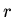 , is assumed to be constant (i.e. is a holonomic
constraint).
, is assumed to be constant (i.e. is a holonomic
constraint).
The kinetic and potential energies are
With 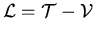 the equation of motion becomes
the equation of motion becomes
giving the equation of motion:
We will discuss the properties of the solutions to the equation of motion
in lecture 13 and lecture
14
SUMMARY
We have defined the Lagrangian
and derived the Lagrangian equations of motion
where 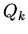 are generalized nonconservative forces. If all forces are
conservative
are generalized nonconservative forces. If all forces are
conservative 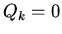 .
.
Example problems: See problems 1
and 2 of 1999 midterm, with solution, problem
set 3, 2000, with solution, problem
set 4 2001, with solution, question 2 of 2001 midterm, with solution.
Return to title page



Next: About this document ...
Birger Bergersen 2002-02-02 
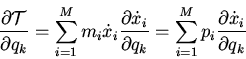
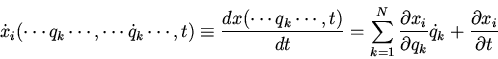
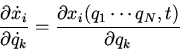
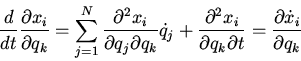
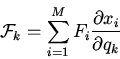
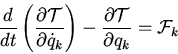
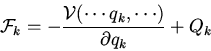
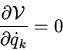
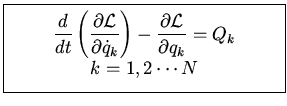
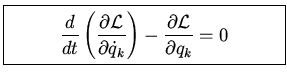
![\begin{displaymath}{\cal T}=\frac{M\dot{X}^2}{2}+\frac{m}{2}[(\dot{X}+\dot{s}\cos\alpha)^2
+\dot{s}^2\sin^2\alpha]\end{displaymath}](lagrangean_files/img30.gif)