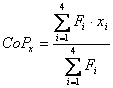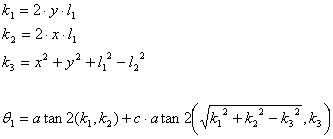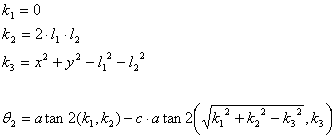|

|
Desenvolvimento de Algoritmos de Controlo para
Locomoção de um Robot Humanóide
Relatório Final de Projecto
Pedro Ferreira Nº27593
Orientação:
Prof. Dr. Filipe Silva (DETI-IEETA)
Prof. Dr. Vítor Santos (DEM-TEMA)
Universidade de Aveiro
Departamento de Electrónica, Telecomunicações e
Informática, IEETA
Licenciatura em Engenharia
Electrónica e Telecomunicações
Julho de 2007
|
Índice
1 Introdução. 5
1.1 Projecto Humanóide da Universidade
de Aveiro (PhUA) 5
1.2 Objectivos. 8
1.3 Estrutura do relatório. 8
2 Enquadramento geral 9
2.1 Protocolo de comunicações. 9
2.1.1 Comunicações CAN.. 11
2.1.2 Comunicação RS-2321 11
2.2 Controlo Local 19
2.2.1 Controlador PID.. 20
2.2.2 Avaliação de Resultados. 26
3 Algoritmos de controlo
baseados em realimentação sensorial 28
3.1 Controlador baseado nas forças de
reacção. 28
3.1.1 Sensores de força: Extensómetros. 28
3.1.2 Controlador usando a matriz Jacobiana. 30
3.1.3 Testes e Resultados. 33
3.2 Controlador da postura da anca. 37
3.2.1 Sensores de inclinação: Inclinómetros. 37
3.2.2 Controlador proporcional 39
3.2.3 Testes e Resultados. 41
3.2.4 Avaliação de Resultados. 47
4 Planeamento do movimento:
padrões de locomoção. 49
4.1 Planeamento de trajectórias. 51
4.1.1 Cinemática directa. 52
4.1.2 Cinemática Inversa. 53
4.2 Locomoção bípede. 55
4.2.1 Fase 1: preparar o movimento. 56
4.2.2 Fase 2: inicio do passo. 56
4.2.3 Vários Passos. 57
4.3 Rotação sobre si próprio. 58
4.4 Pontapé. 62
5 Simulador TwoLegs_22dof 64
5.1 GUI em Matlab. 64
5.1.1 Ambiente de desenvolvimento. 65
5.1.2 Estrutura do Script 66
5.2 Definições estruturais. 69
5.2.1 Dimensões dos elos. 69
5.2.2 Massa dos componentes do robô
Humanóide. 69
5.2.3 Centros de Massa. 70
5.2.4 Relação de transmissão. 71
5.3 TwoLegs_22dof 73
5.3.1 Componentes. 73
5.3.2 Estruturas de suporte ao GUI 79
5.3.3 Organização da aplicação. 84
5.3.4 Ficheiros envolvidos. 86
5.4 GestMovs. 95
5.5 Bugs detectados. 96
6 Conclusão. 97
7 Bibliografia. 98
8 Índice de Imagens. 99
9 Índice de Tabelas. 102
O ser humano, dada a sua capacidade intelectual e sentido
inventivo, desde cedo sentiu necessidade de automatizar tarefas do dia-a-dia.
Episódios de máquinas mecânicas que realizavam tarefas repetitivas ou que
simplesmente entretinham os mais curiosos pela inovação são comuns em toda a
história da humanidade. A evolução dotou-nos de um conjunto de ferramentas cada
vez mais precisas e robustas permitindo-nos cada vez mais explorar a nossa
imaginação na criação artificial.
Não há dúvida de que a ergonomia do ser humano é bastante
versátil, permitindo-nos usar os nossos membros para um vasto leque de tarefas,
desde movimentos de precisão a tarefas mais rudes e pesadas. É esta
característica que nos dá a motivação para criar seres semelhantes a nós, com a
mesma capacidade de adaptação a novos ambientes e capazes de colonizar mundos.
A concepção de robôs humanóides não se fica só por sonhos de
ficção científica. Ao desenvolver-se capacidades humanas em dispositivos
mecânicos está-se a criar alternativas reais de substituição de membros ou
órgãos humanos danificados por dispositivos mecânicos capazes de reproduzir as
capacidades reais e suprir os problemas existentes.
Estas são razões mais que suficientes para a dedicação e
interesse da Universidade de Aveiro num projecto desta envergadura, numa área
que actualmente é meramente académica, com o intuito de deixar marcas e feitos
na evolução de algo grandioso que um dia poderá ser tão comum como um simples
aparelho de televisão em nossas casas.
O projecto de um robô humanóide na Universidade de Aveiro
está a ser desenvolvido desde 2002/2003. É um projecto de cooperação entre o
Departamento de Engenharia Mecânica e o Departamento de Electrónica,
Telecomunicações e Informática.
Do ponto de vista mecânico, destaca-se na plataforma
humanóide um conjunto de 22 graus de liberdade, distribuídos da seguinte forma:
 ·
2 em cada pé (2x2);
·
2 em cada pé (2x2);
 ·
1 em cada joelho (1x2);
·
1 em cada joelho (1x2);
 ·
3 em cada anca (3x2);
·
3 em cada anca (3x2);
 ·
2 no tronco (2x1);
·
2 no tronco (2x1);
 ·
3 em cada braço (3x2);
·
3 em cada braço (3x2);
 ·
2 no suporte da câmara (cabeça) (2x1).
·
2 no suporte da câmara (cabeça) (2x1).

Ilustração 1‑1 – Robô Humanóide da Universidade de Aveiro
A estrutura é constituída essencialmente por alumínio e aço
nos eixos e outros pequenos componentes, pesando um total de 6kg com as
baterias incluídas, e medindo cerca de 60cm. Estes valores foram estabelecidos
de acordo com as regras impostas pelo RoboCup, baseando-se no pressuposto de
que para valores superiores a estes, o uso de servomotores de baixo custo
poderá tornar-se inviável dada a impossibilidade de conciliar binários de
motores e pesos dos equipamentos e acessórios como as baterias.
Para ajudar no controlo, o robô humanóide é dotado de um
conjunto de sensores distribuídos ao longo da estrutura, são eles:
 Sensores
de posição - Os sensores de posição
são potenciómetros que indicam a posição angular actual do servomotor. Há um
sensor de posição por cada servomotor.
Sensores
de posição - Os sensores de posição
são potenciómetros que indicam a posição angular actual do servomotor. Há um
sensor de posição por cada servomotor.
 Sensores
de força - Os sensores de força
estão localizados em pequenas placas distribuídas pelos quatro cantos de cada
pé. Estes sensores servem para medir em cada instante o ponto do centro de
pressão (CoP) nesse pé.
Sensores
de força - Os sensores de força
estão localizados em pequenas placas distribuídas pelos quatro cantos de cada
pé. Estes sensores servem para medir em cada instante o ponto do centro de
pressão (CoP) nesse pé.
 Sensores
de inclinação - Os inclinómetros ou
sensores de inclinação situam-se na zona da anca e servem para indicar a
inclinação da anca em relação ao plano da terra
Sensores
de inclinação - Os inclinómetros ou
sensores de inclinação situam-se na zona da anca e servem para indicar a
inclinação da anca em relação ao plano da terra
 Giroscópios - Os giroscópios ainda não
têm uma aplicação específica. Estes sensores medem a velocidade angular
Giroscópios - Os giroscópios ainda não
têm uma aplicação específica. Estes sensores medem a velocidade angular
 Câmara
CCD - A câmara CCD é os
olhos do humanóide
Câmara
CCD - A câmara CCD é os
olhos do humanóide
Optou-se por um tipo de arquitectura de controlo distribuída
para o desenvolvimento de todo o sistema. O modo de funcionamento desta
arquitectura baseia-se num controlo por módulos que implica a localização de
pequenas unidades estrategicamente posicionadas e que façam a gestão de tarefas
locais. Dessa forma, o sistema é constituído por três tipo de unidades:
 Unidade
Central
Unidade
Central
 Master
Control Unit (MCU)
Master
Control Unit (MCU)
 Slave Control Unit (SCU)
Slave Control Unit (SCU)
A Unidade Central é uma unidade singular responsável pela
gestão global de toda a estrutura. Esta unidade é responsável por enviar
comandos de controlo com impacto em todo o sistema. É também responsável pelo
processamento e gestão da visão.
O Master Control Unit serve de interface entre a unidade
central e as SCU, é um único dispositivo que serve de distribuidor dos comandos
enviados pela Unidade Central.
As Slave Control
Unit tem a função de controlo local, há ao todo 8 espalhadas pelo Humanóide
cada uma com capacidade para actuação directa de 3 servomotores e também pela
leitura dos sensores existentes na sua área de actuação.
Para a comunicação entre os diferentes tipos de unidades,
estão definidos dois barramentos, um série RS-232 que permite uma comunicação
bidireccional ponto a ponto entre a Unidade Central e o MCU e um barramento CAN
(Controller Area Network), que permite a comunicação multi-ponto entre o MCU e
as SCU.
Este trabalho tem como objectivo o estudo de soluções a
aplicar a robôs humanóides. Nesse contexto e, como este é um trabalho de
continuidade, os objectivos definidos destinam-se a atingir patamares de
desenvolvimento. O processo de desenvolvimento a aplicar é começar a partir do
trabalho realizado em anos anteriores, acrescentar mais valias, apontar e
corrigir defeitos e integrar novos componentes.
Os objectivos propostos inicialmente foram os seguintes:
 Continuar
o estudo do controlador local PID.
Continuar
o estudo do controlador local PID.
 Continuar
o estudo dos sensores de força e encontrar situações de uso real durante as
movimentações do robô humanóide;
Continuar
o estudo dos sensores de força e encontrar situações de uso real durante as
movimentações do robô humanóide;
 Iniciar
o estudo dos sensores de inclinação, implementar algoritmos de controlo
baseados na informação por eles fornecida;
Iniciar
o estudo dos sensores de inclinação, implementar algoritmos de controlo
baseados na informação por eles fornecida;
 Estudar
e implementar padrões de locomoção aplicáveis na prática a este robô humanóide;
Estudar
e implementar padrões de locomoção aplicáveis na prática a este robô humanóide;
 Criar
uma interface visual que permita uma interacção user-friendly com o robô.
Criar
uma interface visual que permita uma interacção user-friendly com o robô.
Para a abordagem aos objectivos proposto, o trabalho
encontra-se encadeado hierarquicamente, começando pela base que corresponde ao
enquadramento geral e ao estado de desenvolvimento inicial do projecto,
seguindo depois pela inovação criada durante este ano de trabalho no projecto e
acabando com a integração geral de todo o trabalho ao expor a plataforma de
simulação criada.
Espera-se com esta abordagem criar um nível de conhecimento,
referente ao projecto, suficiente para ter uma panorâmica geral de todo o
trabalho sem no entanto entrar em grandes pormenores técnicos susceptíveis de
aborrecer o mais entusiasta dos leitores.
Nesta secção é discutido o estado inicial de desenvolvimento
do sistema. São abordados temas como o protocolo de comunicações existente e os
controladores de posição usados.
O protocolo de comunicações é a base sobre a qual todo o
sistema assenta, nas secções seguintes descrever-se-á de uma forma geral como
todo o sistema está interligado e quais são os comandos de comunicação
existentes. Este protocolo sofreu durante este ano uma evolução de forma a
integrar novas necessidade ao nível da comunicação.
Há dois tipos de controlo de posição, um designado de malha
aberta e o controlador de posição PID. O controlador de malha aberta,
correspondente ao controlo electrónico integrado nos próprios servomotores não
vai ser abordado no âmbito desta análise porque já está suficientemente
explorado em relatórios anteriores.
Como já foi referido, há três tipos de unidade e uma delas
serve de intermediário entre as outras duas. Esta unidade intermediária é o Master
Control Unit (MCU), também designado por unidade distribuidora. Este nome é-lhe
atribuído por nela serem armazenados os dados de actuação, quer os invariáveis
quer os enviados pela unidade principal (posição, velocidade, …), esses dados
são então reencaminhados para as Slave
Control Unit (SCU) de forma a estas cumprirem com as ordens pedidas.
Há portanto dois protocolos de comunicação em todo o
sistema, um que corre sobre o barramento RS-232 entre a unidade principal e o
MCU e um segundo protocolo estabelecido sobre um barramento CAN comum a todas
as unidades SCU e ligado ao MCU.
As necessidades de comunicação existentes prendem-se com
pretensões de actuação ou de leitura de algumas variáveis associadas
directamente a cada slave. As
funcionalidades que o protocolo de comunicações fornece são:
 Leitura
de sensores
Leitura
de sensores
o
Sensores de posição dos servos;
o
Sensores
de força dos pés;
o
Inclinómetros
ou giroscópios;
 Leitura
de parâmetros dos servos:
Leitura
de parâmetros dos servos:
o
Posição;
o
Velocidade;
o
Corrente;
 Parâmetros
de actuação
Parâmetros
de actuação
o
Posição das juntas;
o
Centro de Pressão de referencia (CoPref);
o
Tempo da trajectória;
o
Activação de PWM;
 Tipo
de controlador de primeiro nível;
Tipo
de controlador de primeiro nível;
 Parâmetros
de controlo;
Parâmetros
de controlo;
o
Ki;
o
Kp;
o
K – ganho do controlador de primeiro nível.
Alguns destes parâmetros circulam sobre os mesmos campos e
estão dependentes de outros para serem identificados como tal. Quer isto dizer,
por exemplo, que o CoPref, vai no mesmo campo que a posição das
juntas mas para ser lido como CoPref têm que estar activo o
controlador correspondente aos sensores de força. Uma descrição dos comandos de
acesso e actuação sobre estes parâmetros é dada na Secção 2.1.2.
O CAN, por ser um
sistema de comunicação série multi-ponto é ideal para interligar todas as
unidades de baixo nível (slaves e master).
Este tipo de comunicação possibilita
assim, o tipo de arquitectura de controlo aplicada à plataforma humanóide.
Em relação às
comunicações CAN importa referir são enviadas ciclicamente mensagens CAN com os
parâmetros de actuação para cada uma das slaves.
Este ciclo é executado de 8 em 8ms (são permitidos ligeiros desvios no caso de
erros na comunicação). Isto permite que seja dedicado 1ms a cada slave, durante o qual, são enviadas duas
mensagens do master para a uma slave com a informação de actuação e,
por cada mensagem recebida, a slave
devolve uma resposta com os seus dados sensoriais. São assim trocadas 4
mensagens entre o MCU e uma SCU.
Os parâmetros de
actuação enviados do master para as slaves, são os que ele possui
actualizados na sua base de dados interna. Quer isto dizer que quer haja pedido
de actuação especificados pela unidade principal ou não, a influência que têm
sobre a comunicação CAN é inexistente, pois esta limita-se a enviar periodicamente
os últimos dados de actuação guardados.
O protocolo de comunicações estabelecido entre o MCU e a
unidade principal precisa de uma análise mais profunda, já que é sobre esta
comunicação que praticamente todo o trabalho desenvolvido corre.
A comunicação RS-232 entre o PC e o MCU
é efectuada assincronamente e é orientada ao byte (start bit+8 bits+stop bit), ou seja, é
transmitido um byte de dados em cada transmissão/recepção. Pretende-se que numa
única mensagem esteja contida toda a informação relativa a um parâmetro a
ler/actuar das três juntas de um SCU, o que implica que cada mensagem seja
constituída por vários bytes.
2.1.2.1 Device
drivers
Sem entrar em muitos
pormenores técnicos sobre como está desenvolvido a comunicação RS-232,
interessa salientar os device drivers
que são disponibilizados para ler/actuar sobre as SCU. As funções existentes
abrangem desde o estabelecimento da comunicação, passando pelo teste às
ligações até ao envio de parâmetros de actuação ou leitura. Estes comandos
estão desenvolvidos em
Matlab. Temos assim as seguintes funções:
 As
funções initcom e killcom servem exclusivamente para abrir
e fechar, respectivamente, a porta série que é utilizada pela unidade
principal.
As
funções initcom e killcom servem exclusivamente para abrir
e fechar, respectivamente, a porta série que é utilizada pela unidade
principal.
|
Initcom
|
|
Estabelecimento
de uma nova ligação via RS-232
|
|
[handler,state]=initcom(gate,rate)
|
|
Entradas:
gate -> Porta a utilizar (1,2,...)
rate -> baudrate a definir (bits/s)[i]
Saídas:
handler -> ID da linha de comunicações
state -> Configurações da linha
|
O baudrate usado para a comunicação
com o master é de 115200bps.
|
Killcom
|
|
Término
de uma ligação RS-232 existente.
|
|
stat=killcom(handler)
|
|
Entradas:
|
|
handler -> ID da linha série
|
|
Saídas:
stat -> retorna 1 em caso de sucesso
|
 A
função testcom faz um pedido ao master de envio de uma sequência predefinida,
aguarda a sua recepção e verifica se houve erros na transmissão. No caso de não
haver erros o retorno desta função é zero.
A
função testcom faz um pedido ao master de envio de uma sequência predefinida,
aguarda a sua recepção e verifica se houve erros na transmissão. No caso de não
haver erros o retorno desta função é zero.
|
Testcom
|
|
Pedido
de envio de uma sequencia de teste.
|
|
[error,errorstr]=testcom(H)
|
|
Entradas:
|
|
handler -> ID da linha série
|
|
Saídas:
error
-> Código de erro
errorstr -> String descritiva do erro
|
 A
função readcanstat permite a verificação das comunicações CAN
A
função readcanstat permite a verificação das comunicações CAN
|
Readcanstat
|
|
Leitura
do estado do barramento CAN.
|
|
[array,state,rx,error,errorstr]=readcanstat(H)
|
|
Entradas:
|
|
handler -> ID da linha série
|
|
Saídas:
array ->
[estado de erro, #erros de transmissão, #erros de recepção]
state ->
Bits de estado dos servos
rx ->
Mensagem de baixo nível recebida
error ->
Código de erro, se existente
errorstr -> String descritiva do erro
|
 Para
a leitura da informação actualmente existente na SCU, há duas funções, readjoint e readspecial. A primeira permite a leitura de parâmetros associados
ao servomotor, como a posição ou a corrente consumida actual, Tabela
2‑1. A segunda função permite a leitura dos sensores
especiais que estão acoplados ao circuito de piggy-back, como por exemplo os sensores de força ou de inclinação.
Para
a leitura da informação actualmente existente na SCU, há duas funções, readjoint e readspecial. A primeira permite a leitura de parâmetros associados
ao servomotor, como a posição ou a corrente consumida actual, Tabela
2‑1. A segunda função permite a leitura dos sensores
especiais que estão acoplados ao circuito de piggy-back, como por exemplo os sensores de força ou de inclinação.
|
Readjoint
|
|
Leitura
de um parametro sensorial dos servos de um SCU
|
|
[servos,state,rx,error,errorstr]=readjoint(H,scu_id,param)
|
|
Entradas:
H => Handler para
comunicar com o Master
scu_id => Identificador do SCU alvo
param => Parametro a ler (Tabela
2‑1)
Saídas:
servos => Parametro de saída
[servo1,servo2,servo3]
state => Bits de estado dos servos (Tabela
2‑2)
rx => Mensagem de baixo nível recebida
error => Código de erro, se existente
errorstr => String descritiva do erro
|
|
Campo
param
|
Descrição
|
Campo servos
|
Unidades
|
|
PARAM_POSITION
|
0
|
Posição angular de cada junta.
|
[pos1,
pos2, pos3]
|
Graus
|
|
PARAM_VELOCITY
|
1
|
Velocidade estimada de cada junta.
|
[vel1,
vel2, vel3]
|
Graus/100ms
|
|
PARAM_CURRENT
|
2
|
Corrente drenada por cada servo.
|
[curr1,
curr2, curr3]
|
% do T de PWM
|
Tabela 2‑1 - Valores possíveis do parâmetro param da
função readjoint
|
Elemento
|
Campo
|
Descrição
|
|
1
|
PWM
|
Activo se todos os motores possuem o PWM ligado.
|
|
2
|
Calib
|
Calibração dinâmica da posição dos servos activada.
|
|
3
|
Deadline
|
Ocorrência de um erro de violação da largura de banda
disponível.
|
|
4
|
FinAll
|
Todos as juntas terminaram a trajectória.
|
|
5
|
FinOne
|
Pelo menos uma das juntas terminou a trajectória.
|
|
6
|
FinServo3
|
A junta 3 terminou a trajectória.
|
|
7
|
FinServo2
|
A junta 2 terminou a trajectória.
|
|
8
|
FinServo1
|
A junta 1 terminou a trajectória.
|
Tabela 2‑2 - Valores presentes no vector status
retornado pela função readjoint
|
Readspecial
|
|
Leitura
dos sensores especiais (sensores de força, giroscópio ou inclinómetro).
|
|
[special,rx,error,errorstr]=readspecial(H,scu_id)
|
|
Entradas:
H => Handler das comunicações com o Master
scu_id => Identificador do SCU alvo
Saídas:
special => Valores dos sensores especiais
rx => Mensagem de baixo nível recebida
error => Código de erro, se existente
errorstr => String descritiva do erro
|
A escolha do sensor que se pretende ler está depende do scu_id a que se está a aceder, pois uma slave só tem um tipo de sensor especial
acoplado ao seu circuito de piggy-back.
 Como
funções de actuação são disponibilizados dois tipos de comandos, o applyjoint que permite o envio de
posições, velocidade ou simplesmente de activação do PWM nos servomotores e, o applycontrol que permite designar o tipo
de controlador activo e os parâmetros que definem esse controlador.
Como
funções de actuação são disponibilizados dois tipos de comandos, o applyjoint que permite o envio de
posições, velocidade ou simplesmente de activação do PWM nos servomotores e, o applycontrol que permite designar o tipo
de controlador activo e os parâmetros que definem esse controlador.
|
Applyjoint
|
|
Aplicação de uma ordem de actuação a cada
componente de um SCU.
|
|
[rx,error,errorstr]=applyjoint(H,scu_id,param,servos)
|
|
Entradas:
H => Handler para comunicar com o Master
scu_id => Identificador do SCU alvo
param => Parametro a aplicar (Tabela
2‑3)
servos => Dados a aplicar
[servo1,servo2,servo3]
Saídas:
rx => Mensagem de baixo nível recebida
error => Código de erro, se existente
errorstr => String descritiva do erro
|
|
Campo
param
|
Descrição
|
Campo servos
|
Unidades
|
|
PARAM_POSITION
|
0
|
Posição referência a ser atingida.
|
[ref1,
ref2, ref3]
|
Graus ou outro
|
|
PARAM_VELOCITY
|
1
|
Duração do movimento a efectuar.
|
[vel1,
vel2, vel3]
|
Ciclos de 20ms
|
|
PARAM_SPECIAL
|
3
|
Activação/desactivação do PWM aplicado aos motores.
|
[0/1, 0, 0]
|
(Valor booleano)
|
Tabela 2‑3 - Valores possíveis do parâmetro param na
função applyjoint
|
Applycontrol
|
|
Selecção
do controlador de primeiro nível e ajuste dos seus parâmetros bem como dos
parâmetros do controlador local
|
|
[rx,error,errorstr]=applycontrol(H,scu_id,param,servos)
|
|
Entradas:
H => Handler para comunicar com o Master
scu_id => Identificador do SCU alvo
param => Parametro a modificar (Tabela
2‑4)
servos => Dados a aplicar
[servo1,servo2,servo3]
Saídas:
rx => Mensagem de baixo nível recebida
error => Código de erro, se existente
errorstr => String descritiva do erro
|
|
Campo
param
|
Descrição
|
Campo servos
|
|
PARAM_KI
|
0
|
Ganho da componente integral (Ki) do
controlador local.
|
[Ki1,
Ki2, Ki3]
|
|
PARAM_KP
|
1
|
Ganho da componente proporcional (Kp) do
controlo local.
|
[Kp1,
Kp2, Kp3]
|
|
PARAM_K
|
2
|
Ganho (K) do controlador de primeiro nível.
|
[K1,
K2, K3]
|
|
PARAM_CONTROLON
|
3
|
Tipo de controlo de primeiro nível (Type) a
aplicar em cada junta (Tabela 2‑5).
|
[Type1, Type2, Type3]
|
Tabela 2‑4 - Valores possíveis do parâmetro param na
função applycontrol
Os tipos de controlador de primeiro nível que podem ser
especificados na função applycontrol
estão descritos na Tabela 2‑5.
|
Tipo de
Controlo (Type)
|
Descrição
|
|
NO_CONTROL
|
0
|
Sem Controlo de
primeiro nível
|
|
COP_CONTROL
|
1
|
Controlo de Centro
de Pressão
|
|
INC_CONTROL
|
2
|
Controlo de
Inclinação
|
|
GIRO_CONTROL
|
3
|
Controlo de velocidade angular
|
Tabela 2‑5 - Tipo de controladores de primeiro nível
2.1.2.2 Funções
auxiliares
Os comandos existentes para comunicação RS-232 são
excelentes quando se pretende actuar uma unidade slave mas na actuação a várias slaves
é necessário haver um conjunto de funções de nível superior que actuem de forma
mais eficiente. Pretende-se com isso que seja permissível definir vários
parâmetros em diferentes slaves só
com uma função, dessa forma foram criadas um conjunto de funções auxiliares à
actuação nas slaves.
Estas funções foram criadas conforme as necessidades
sentidas ao longo do tempo, o que justifica o facto de não serem o mais
eficientes possível nas suas utilidades, isto é, há algumas funções que podem
fazer trabalhos semelhantes, ou serem demasiado específicas.
 Para
activar e desactivar o PWM de várias SCU:
Para
activar e desactivar o PWM de várias SCU:
|
activaPWM
|
|
Activa
o PWM dos servos das slaves mencionadas
|
|
erro=activaPWM(handler,
varargin)
|
|
Entradas:
handler => Handler para comunicar com o Master
varargin:
[] => Activa o PWM das 8 SCUs
SCU1, SCU2,… => Activa o PWM das SCU indicadas
Saídas:
erro => Indica se houve erros ou não
|
|
desactivaPWM
|
|
Desactiva
o PWM dos servos das slaves mencionadas
|
|
erro=desactivaPWM(handler,
varargin)
|
|
Entradas:
handler => Handler para comunicar com o Master
varargin:
[] => Desactiva o PWM das 8 SCUs
SCU1, SCU2,… => Desactiva o PWM das SCU
indicadas
Saídas:
erro => Indica se houve erros ou não
|
 Para
definir a mesma velocidade para os servos de diferentes SCU
Para
definir a mesma velocidade para os servos de diferentes SCU
|
defineVel
|
|
Permite
definir a velocidade para vários servos
|
|
erro
= defineVel(handler, vel, varargin)
|
|
Entradas:
handler => Handler para comunicar com o Master
Vel => Velocidade que se pretende aplicar
varargin:
[] => Aplica a mesma velocidade aos servos das
8 SCUs
SCU1, SCU2,… =>Aplica a mesma velocidade aos
servos das SCU indicadas
Saídas:
erro => Indica se houve erros ou não
|
 Para
aplicar valores de um tipo especifico a todos os servos de todas as slaves
Para
aplicar valores de um tipo especifico a todos os servos de todas as slaves
|
aplicaConf
|
|
Permite
aplicar vários tipos de configurações a todos os servos
|
|
erro
= aplicaConf(handler, tipo, valMat)
|
|
Entradas:
handler => Handler para comunicar com o Master
tipo => parâmetro a aplicar (ver Tabela
2‑6)
valMat => Matriz com os valores para todos os
servos
Saídas:
erro => Indica se houve erros ou não
|
|
Parâmetro
|
Descrição
|
|
0
|
Posição
|
|
1
|
Velocidade
|
|
2
|
Parâmetro ki do controlador local
|
|
3
|
Parâmetro kp do controlador local
|
|
4
|
Ganho do controlador de primeiro
nível
|
|
5
|
Tipo de
controlador de primeiro nível
|
Tabela 2‑6 - Tipo de parâmetro para aplicaConf
 Para
ler um parâmetro em todas as slaves
Para
ler um parâmetro em todas as slaves
|
lerParam
|
|
Permite
ler o mesmo parâmetro de todos os servos
|
|
valMat
= lerParam(handler, tipo)
|
|
Entradas:
handler => Handler para comunicar com o Master
tipo => parâmetro a ler (ver Tabela
2‑7)
Saídas:
valMat => Matriz com os valores para todos os
servos
|
|
Parâmetro
|
Descrição
|
|
0
|
Posição
|
|
1
|
Velocidade
|
|
2
|
Corrente consumida pelo servo
|
|
3
|
Sensores
especiais
|
Tabela 2‑7 - Tipo de parâmetro a ler em lerParam
Para a actuação das juntas é essencial tanto o controlo de
posição como de velocidade, e dado que em média cada junta não possui uma
excursão de movimento superior a 180º, uma solução baseada em servomotores foi
a mais imediata. Podem-se enunciar as seguintes vantagens e desvantagens para
esta escolha:
D
Excursão de posição de 180º;
C
Controlador de posição incluído;
C
Relativamente pequeno e compacto;
C
Relativamente barato;
D
Não oferece controlo de velocidade.
Os servomotores escolhidos como elemento de actuação nas
juntas são da HITEC, modelo HS-805BB cuja tabela de especificações está
representada na Ilustração 2‑1.


Ilustração 2‑1 - Servomotor
HITEC HS-805BB
Este servomotor destaca-se por possuir um binário máximo de
2.42, mas ficando ainda assim aquém do binário máximo necessário (segundo
simulações) para o pior cenário de actuação. A forma de se aumentar o binário é
utilizando engrenagens de transmissão, sacrificando por outro lado velocidade e
gama de excursão do servomotor. Esta foi a solução adoptada para compensar a
necessidade de binários superiores ao fornecido pelo servomotor. Dessa forma,
estão dispostas em todas as juntas da estrutura polias (engrenagens) de
transmissão com uma relação que varia de 1, 2.5 ou 3,75. A transmissão do binário
é efectuada por correias (Ilustração
2‑2).

Ilustração 2‑2 - Polias de transmissão existentes ao longo
da estrutura
Para o controlo de posição existem duas possibilidades:
 Controlo
electrónico existente nos servos, designado por controlo em malha aberta, pois
este controlador não é acessível pelas slaves.
Controlo
electrónico existente nos servos, designado por controlo em malha aberta, pois
este controlador não é acessível pelas slaves.
 Controlador
PID (Proporcional+Integrador+Derivativo), com os seus parâmetros directamente
acessíveis pela Unidade Principal.
Controlador
PID (Proporcional+Integrador+Derivativo), com os seus parâmetros directamente
acessíveis pela Unidade Principal.
O controlo em malha aberta, por ser inatingível via software
não será abordado no contexto deste relatório isto porque toda a sua estrutura
já foi apresentada e analisada em anos anteriores.
Na continuação do trabalho que tinha sido desenvolvido no
ano anterior, continuou-se na procura dos parâmetros PID que melhor se aplicam
ao trabalho dos servomotores.
Para auferir os parâmetros do controlador PID, recorreu-se
ao método sugerido no ano anterior:
1.
Aumentar KI, de modo a optimizar o tempo de atraso, até começar a ocorrer
overshoot;
2.
Aumentar o valor de KP o suficiente para eliminar o overshoot. Não convém
utilizar este parâmetro para optimizar o tempo de atraso, uma vez que o tempo
de estabelecimento é, ao mesmo tempo, agravado. Deixemos, por isso, essa tarefa
à acção integral;
3.
Se a resposta transitória ainda não for demasiado
oscilante, voltar ao passo 1 para melhorar ainda mais o tempo de atraso;
4.
Se começar a instabilizar durante a fase transitória,
aumentar o parâmetro KD de
modo a conferir suavidade durante o percurso;
5.
Voltar ao passo 1.
Para isso foi criado
o GUI ControlTest, Ilustração
2‑3, que permite seleccionar os parâmetros do
controlador e verificar os resultados obtidos para uma trajectória definida.
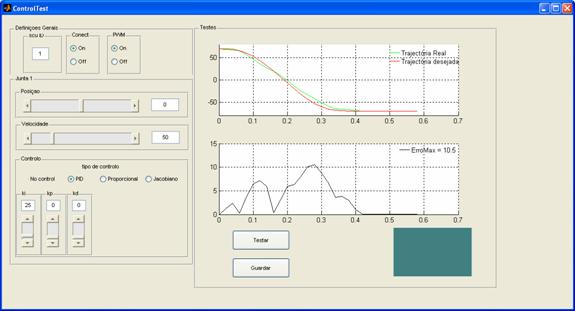
Ilustração 2‑3 - GUI para teste do controlador PID
Esta interface de testes do controlador de posição PID,
permite definir os parâmetros PID, aplicar uma velocidade e realizar o teste de
uma trajectória definida no script de
testes. Os resultados obtidos podem depois ser guardados num ficheiro que
descreve os parâmetros usados.
No entanto, este teste só é aplicável a um servo e, como
essa experiência já tinha sido desenvolvida no ano anterior, optou-se por
realizar uma análise do controlador com movimentos articulados de várias
juntas.
Utilizou-se toda a perna do robô para encontrar os
parâmetros PID passíveis de realizar a trajectória do movimento mais próxima
possível do previsto. O movimento utilizado para o teste foi o de flexão de uma
perna, Ilustração
2‑4. Nesse movimento são envolvidos os servos do
tornozelo, do joelho e o da anca.




Ilustração 2‑4 - Movimento de flexão de uma perna
Numa primeira fase do teste não se colocou carga na anca e
só se aplicou o controlador PID à junta do tornozelo e à junta do joelho,
estando a junta da anca em malha aberta. Os parâmetros foram ajustados segundo
o método proposto até obter a resposta apresentada na Ilustração
2‑5 até à Ilustração 2‑7.
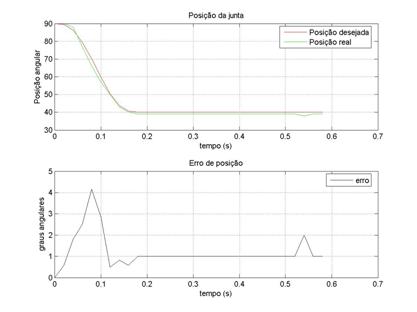
Ilustração 2‑5 – Junta do tornozelo com ki=20 kp=20 kd=5
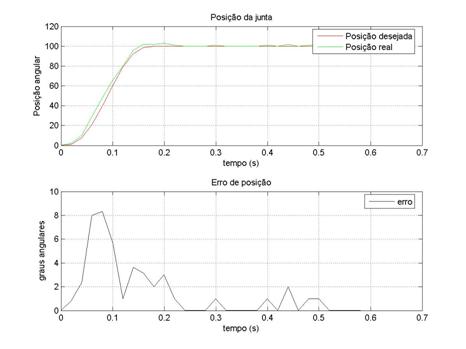
Ilustração 2‑6 Junta do joelho com ki=20 kp=20 kd=0
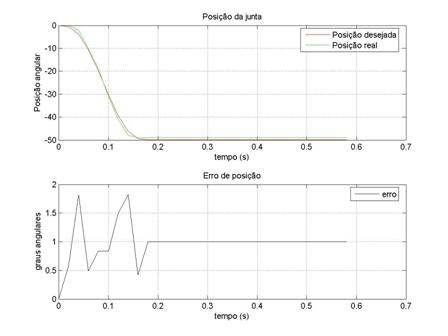
Ilustração 2‑7 – Junta da anca em malha aberta
Nesta primeira experiência estão representadas as
trajectórias dos 3 servos que perfazem o movimento de flexão de perna. Esta é a
resposta do controlador com os parâmetros PID ajustados.
Efectuando a mesma experiência mas com uma carga total na
anca de 713g, mantiveram-se os parâmetros PID para comparar a sua resposta. Desta
vez activou-se o controlador PID da junta da anca porque agora suportava uma
carga. Os resultados obtidos estão representados da Ilustração
2‑8 até Ilustração 2‑10.
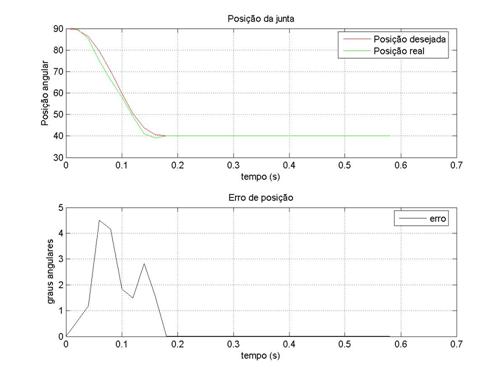
Ilustração 2‑8 – Junta do tornozelo com ki=20 kp=20 kd=5
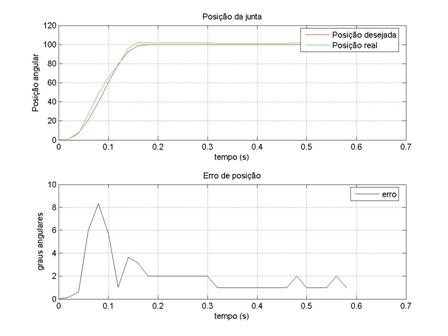
Ilustração 2‑9 – Junta do joelho com ki=20 kp=20 kd=0
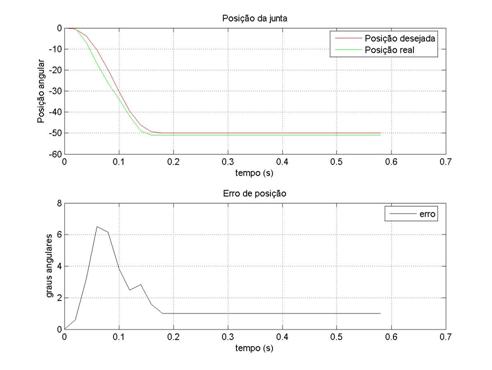
Ilustração 2‑10 – Junta da anca com ki=30 kp=15 kd=0
Numa análise comparativa, junta a junta, pode-se observar
que não há muitos desvios nas suas respostas. O caso mais expressivo de
divergência entre resposta esperada e obtida é a junta da anca, que na
experiência anterior não tinha o controlador activo e nesta nova experiência,
com controlador, revelou uma resposta mais rápida do que o esperado.
Apesar do resultado
promissor, há que lembrar que a carga imposta era de somente 713g, muito abaixo
da carga máxima que a perna terá de suportar, que é de aproximadamente 5kg.
Muito embora a necessidade da continuação desta experiência com cargas
superiores fosse essencial para obter conclusões mais realistas, tal revelou-se
impossível na altura em que estes testes foram efectuados. Essa impossibilidade
deveu-se à instabilidade da estrutura quando se tentou testar uma carga de 2kg.
Em estudos futuros deve tentar mensurar-se o efeito que o
controlador PID de um servo tem nos outros servos e de que forma é que se pode
tentar isolar essa interferência. A questão das interferências deve ser tida em
conta numa implementação futura desta controlador, porque não se trata de
compensar um servo independente mas sim um sistema relacionado de 22 juntas.
O Graphical User Interface (GUI) criado para o controlo de
um servomotor pode ser facilmente estendido para múltiplos servos de diferentes
slaves. A sua utilização permite de
uma forma simples e interactiva actuar directamente no ajuste dos parâmetros
PID. Na Secção 5, falar-se-á mais sobre possíveis implementações
deste tipo de interfaces gráficas.
Como nota final fica a remoção do parâmetro kd do
controlador PID, passando este a ser só um controlador PI
(Proporcional+Integrador). As razões para esta alteração devem-se à baixa
influência do parâmetro kd no controlo. Associado a este pormenor
estava a necessidade de integrar no protocolo de comunicações RS-232 um campo
que permitisse actuar sobre o controlador de 1º nível (ver Secção 2.1.2). A solução foi usar o campo do parâmetro kd
para esse efeito.
O robô humanóide é dotado de um conjunto de capacidades
sensoriais. Utilizando controladores apropriados, associados aos sinais
provenientes destes sensores pode induzir-se no humanóide um comportamento mais
adaptativo às condições existentes. Assim, há semelhança do ser humano, o
humanóide será capaz de apresentar um movimento baseado na sua experiência
sensorial.
Os sensores em estudo são os sensores de força e os
acelerómetros que sob determinadas condições comportar-se-ão aproximadamente
como inclinómetros.
Os testes efectuados com estes sensores envolveram somente o
uso de uma perna. Espera-se dessa forma, criar condições para no futuro haver
uma implementação dos controladores testados ao nível de toda a plataforma
humanóide.
No seguimento do estudo feito no ano anterior destes
sensores e, dos controladores implementados, procedeu-se este ano à continuação
do estudo e melhoramento desses controladores.
O primeiro contacto com o robô humanóide foi o controlo do
equilíbrio de uma perna baseado na análise dos sensores de força. O robô
humanóide dispõe de 4 sensores de força em cada pé, que se deformam consoante o
peso que estiverem a suportar. Estes sensores são placas de acrílico deformável
com um extensómetro para medir a deformação, Ilustração
3‑1. Não se pretende com este sistema saber a força
exacta exercida sobre o pé mas sim a força relativa, daí que não se use uma
relação directa entre deformação e força aplicada. Os objectivos pretendidos
com estes sensores centram-se no controlo do equilíbrio da perna. O equilíbrio
é-nos fornecido pelo centro de pressão (CoP, ponto de aplicação da força de
reacção resultante no pé).

Ilustração 3‑1 – Placa de acrílico com um extensómetro
colado
Como os sensores, têm aproximadamente o mesmo tipo de
deformação quando sujeitos à mesma força, o raciocínio subjacente ao cálculo do
centro de pressão situa-se numa média pesada de todos os extensómetros. O peso
que cada extensómetro apresenta é um vector com a sua localização em relação ao
centro do pé, isto é a sua posição em xx e yy, Ilustração
3‑2. Isto possibilita que com base no valor dos
extensómetros, desde que previamente calibrados a zero no ponto de referência
(CoPref), se possa derivar a posição relativa em relação a esse
ponto.
Têm-se então que a distância de cada extensómetro ao centro
do pé é dada pelo vector:  . O centro de pressão é definido por uma posição cartesiana
dada por:
. O centro de pressão é definido por uma posição cartesiana
dada por:  , onde, as fórmulas de cálculo do seu valor segundo as suas
duas componentes são dadas pelas equações seguintes:
, onde, as fórmulas de cálculo do seu valor segundo as suas
duas componentes são dadas pelas equações seguintes:
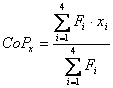
 ( 3‑1)
( 3‑1)
Um problema a salientar destas aproximações é que elas são
calculadas baseando-se numa deformação igual de cada placa face à mesma força
aplicada mas, isso não se verifica na prática, cada placa tem uma recta de
deformação com um declive ligeiramente diferente das outras e, há também as
zonas de não linearidade que não são contempladas. Isto a somar à aproximação
linear da resposta dos extensómetros pode afectar um cálculo preciso do CoP.
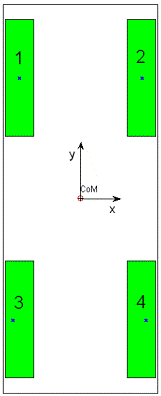
Ilustração 3‑2 – Distribuição dos sensores de força pelo
pé e o referencial usado
Quando se pretende que o CoPref se situe
aproximadamente no centro do pé de suporte, então calibra-se os sensores de força
a zero quando a perna estiver na sua posição vertical (relativamente ao plano
da Terra). Este CoPref é definido como sendo o ponto (0,0) e é
partir daqui que se calculam os erros que alimentam o controlador do CoP.
Pode-se ainda, utilizar o CoPref para definir uma
trajectória da anca e utilizar este tipo de movimento para definir movimentos
mais complexos baseados unicamente na experiência sensorial.
Para a derivação de uma relação matemática entre uma
grandeza linear de distância, CoP, e um parâmetro angular, velocidade, tem de
se recorrer à matriz jacobiana.
 ( 3‑2)
( 3‑2)
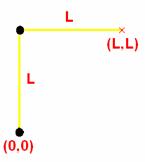
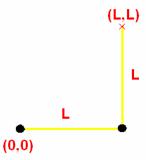
O cálculo destas expressões pode ser feito com base nas Ilustração
3‑3 e Ilustração 3‑4. Nestas figuras, o L representa o comprimento do
elo, o R a distancia entre o início do elo e o seu centro de massa e o M a
massa total do elo.
Com esta matriz, não se pretende só determinar as relações
entre o CoP e a velocidade angular, mas também uma relação entre a última e a
altura da anca.
A derivação das expressões que preenchem esta matriz é
extensa mas facilmente dedutível, por isso são apresentados na Tabela
3‑1, as deduções finais.
Considerando,

Derivadas parciais do CoMy:

Derivadas parciais do CoMx:

Derivadas parciais da altura z:

Tabela 3‑1 - Expressões da matriz jacobiano
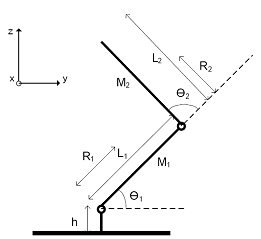
Ilustração 3‑3 – Diagrama representativo de uma perna sob
a vista lateral
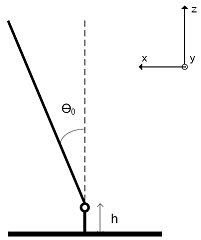
Ilustração 3‑4 – Diagrama representativo de uma perna sob
a vista frontal
A equação de controlo usada, é então:
 , ( 3‑3)
, ( 3‑3)
onde o o “v” é o
incremento a aplicar à junta respectiva, o “Kp”
é um vector com o ganho controlador para cada direcção, o “J-1” é a inversa da matriz
jacobiana e o “e” é o vector com o erro em cada direcção.
Como a inversa da matriz jacobiana teria de ser calculada em
cada instante, porque as posições das juntas variam e, devido ao peso que isso
representa para o processamento duma PIC, optou-se por fazer uma aproximação,
usando a matriz transposta da matriz jacobiana em vez da sua inversa. Dessa
forma a equação de controlo é a mostrada na Equação 3‑1.
 ( 3‑4)
( 3‑4)
O teste realizado com o controlador baseado nos sensores de
força foi alterar de forma constante o CoP de referência de forma a este
perfazer um rectângulo. Este teste foi realizado com o controlador local em
malha aberta e alterando o CoPref de forma à trajectória dar 10
voltas ao rectângulo. Dessa forma pode-se analisar a resposta do controlador
segundo diferentes perspectivas. Os resultados obtidos estão representados nos
gráficos abaixo. Há 4 gráficos diferentes para cada experiência, no primeiro está
representado a trajectória do CoP, nos restantes gráficos tem-se a variação do
CoP segundo as várias componentes (x, y, z), a componente z representa a altura
pretendida para a anca, que também é definida como fazendo parte do CoP.
Usou-se para todas as experiências um ganho Kp de
50, dado que este valor se revelou, em experiências paralelas, ser o mais
ajustado para o controlador. Para todos os casos a perna iniciava-se
completamente esticada.
Para a primeira experiência a velocidade do movimento era de
2s por aresta (Ilustração 3‑5 a Ilustração 3‑8).
Alterou-se na segunda experiência a velocidade do movimento
para 4s por aresta (Ilustração
3‑9 a Ilustração 3‑12).
Para a última experiência colocou-se a velocidade de
movimento a 5s por aresta (Ilustração
3‑13 a Ilustração 3‑16).
Com a diminuição da velocidade de movimento há uma melhoria
da resposta do controlador o que já de esperava à priori. No entanto, há certos
pontos da trajectória prevista que nunca são atingidos. A explicação para esse
sucedido passa pela suposição inicial de que todas as placas têm a mesma curva
de deformação. O que acontece é que nesses pontos da trajectória, a
sensibilidade da placa está ligeiramente superior às outras, não permitindo que
o CoP seja calculado com precisão. Já o contrário também acontece, há pontos da
trajectória que são ultrapassados, isto porque a sensibilidade associada às
placas situadas nesses pontos é inferior às restantes e portanto, tem de haver
uma maior pressão sobre essas placas, para obter a leitura desejada.
Um problema mais explícito passa pelo controlo de altura,
que mantêm um erro muito acima do desejado e, sem grandes alterações durante
todas as experiências. Esta situação ocorre, porque durante este teste a perna
iniciava-se esticada, estando portanto num ponto de singularidade difícil de
sair. Conclui-se daqui, que este ponto de singularidade deve ser evitado no
futuro, quando se activar o controlador do CoP, ou então alterar a matriz jacobiana
de forma a corrigir esta situação.
Uma das restrições habitualmente usadas na definição de
padrões de locomoção é manter a postura da anca sempre constante, permitindo
dessa forma coordenar os movimentos abaixo da anca (pernas) e acima da anca (tronco
e braços), sem que haja interferência directa de uns nos outros.
Para efectuar este controlo da postura da anca de uma forma
adaptativa, à semelhança do que foi feito com o controlo do equilíbrio, faz-se
um controlo com base na inclinação da anca em relação ao plano da Terra. Há
assim dois eixos de inclinação possíveis. Os sensores usados para este tipo de
medida são os inclinómetros já estudados em anos anteriores.
Os inclinómetros são um dispositivo de medida que nos indica
a diferença angular entre a perpendicular do plano do inclinómetro e o vector
da aceleração da gravidade.
Os inclinómetros usados são baseados num acelerómetro, o
ADXL202E da Analog Devices (Ilustração
3‑18). Este acelerómetro é capaz de distinguir
variações da aceleração de ±2g e mede tanto acelerações estáticas como
acelerações dinâmicas. Este instrumento de medida da aceleração usa uma massa
sísmica situada entre dois braços com sensores de força. Dessa forma qualquer
vibração (acelerações dinâmicas) ou força constante (aceleração estática) é
medida por estes sensores.
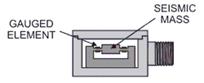
Ilustração 3‑17 - Modo de funcionamento do acelerómetro

Ilustração 3‑18 -
Acelerómetro ADXL202E
Este instrumento é capaz de medir a variação em dois eixos
situados no plano paralelo à superfície da Terra, o pitch e roll. Estes nomes,
derivados da aeronáutica, correspondem ao eixo dos yy e xx, respectivamente,
utilizados para o humanóide, tal como representado na Ilustração
3‑19. Para o cálculo da inclinação sofrida segundo os
eixos xx e yy são usadas as seguintes fórmulas:
 ( 3‑5)
( 3‑5)
 ( 3‑6)
( 3‑6)
A constante “A”
representa um factor de leitura que é adquirido mediante calibração dos inclinómetros.
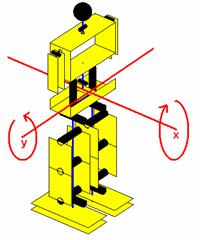
Ilustração 3‑19 - Eixos de inclinação
Os inclinómetros estão posicionados de forma a medir a
inclinação da anca nos dois eixos possíveis, relativamente ao plano da Terra. Os
inclinómetros usados são na realidade acelerómetros que sob determinadas
condições apresentam uma resposta aproximada dos inclinómetros. As condições
necessárias para esse comportamento se verificar é não haver grandes
acelerações dinâmicas na estrutura humanóide, isto porque, a aceleração medida
pelos acelerómetros é a resultante entre a aceleração da gravidade (estática) e
as acelerações dinâmicas. Se se conseguir limitar o segundo termo têm-se uma
medida praticamente relativa só à aceleração da gravidade. É dessa forma que se
pode aproximar a medida do acelerómetro à medição da inclinação real elemento
associado ao acelerómetro.
A relação existente entre a inclinação da anca e as juntas
é:
 ( 3‑7)
( 3‑7)
 ( 3‑8)
( 3‑8)
O pitch e o roll, já foram definidos e indicam a
inclinação segundo o eixo dos yy e dos xx. As variáveis inc_sup_y e inc_sup_x,
representam a inclinação do plano segundo o eixo dos yy e xx, respectivamente.
As variáveis q1, q2, q3, q4 e q5 são as posições angulares das juntas numeradas
de uma perna, tal como representado na Ilustração
3‑20. As constantes 2.5 e 3.75 devem-se à relação de
transmissão que existe entre os servos e as juntas.
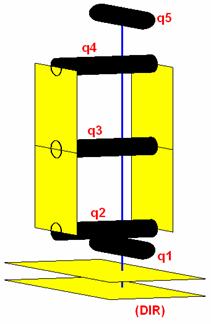
Ilustração 3‑20 – Juntas que influenciam a inclinação da anca
Como para compensar a inclinação da anca só são necessárias
duas juntas, desde que elas actuem sobre o pitch
e o roll e como as 3 primeiras juntas
são usadas pelo controlador de equilíbrio, optou-se por só usar as juntas 4 e 5
para fazer a devida compensação da inclinação da anca.
Dessa forma, através da medida efectuada pelo inclinómetro calcula-se
a inclinação real da anca em relação ao plano da Terra. Se esse valor for
diferente da inclinação da anca pretendida então há um erro que têm de ser
compensado. É usado um controlador proporcional que através do erro medido e
usando uma constante de ganho permite calcular uma saída que corresponda ao
incremento a aplicar à junta de forma a compensar o erro. A função de controlo
segundo o pitch (eixo yy) é dada pela seguinte equação:
 ( 3‑9)
( 3‑9)
Neste caso, o delta é o incremento a aplicar ao servomotor
responsável por compensar a inclinação na direcção em questão, o erro é a
diferença entre a inclinação medida e a inclinação pretendida, o k é o ganho do
controlador, é com este parâmetro que se ajusta a velocidade de actuação e o
2.5 é o valor da relação de transmissão existente entre os servos e a junta.
Esta função só representa o caso em que se compensa o pitch. A resposta deste controlador está representada na Ilustração
3‑21, para um ganho de 0.1 e de 0.5.
Para o caso em que se compensa o roll, a equação do controlador é:
 ( 3‑10)
( 3‑10)
Como os testes efectuados só usaram este controlador para
compensar a inclinação da anca segundo o eixo dos yy (pitch), a equação de
controlo para o eixo dos xx, não está
ainda implementada.
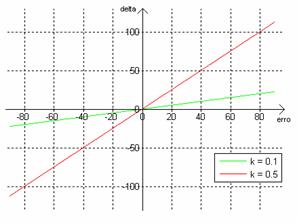
Ilustração 3‑21 – Curva de resposta do controlador segundo
o pitch
A forma mais simples de testar o correcto funcionamento do
controlador foi alterar a inclinação do plano e observar a sua reacção. Um
outro teste realizado foi, utilizando uma repetição de uma trajectória
rectangular realizada pela anca. Como a anca é móvel mas o pé que a suporta
estava fixo, neste teste, então o movimento rectangular implica uma variação de
inclinação da anca. Impôs-se uma inclinação de referência de zero graus e
variaram-se velocidades de movimento e o ganho do controlador.
Ilustração 3‑22- Movimento efectuado no teste do
controlador dos inclinómetros (vista de cima)
Os resultados estão representados nos gráficos que se seguem.
Foram testados diferentes ganhos para o controlador e diferentes velocidades para
o movimento.
Para analisar os resultados estão representados, para cada
experiência, três gráficos. O primeiro refere-se à inclinação da anca, no caso
de não haver compensação, o segundo faz a comparação entre a resposta que era
esperada e a resposta real do servo responsável pela compensação e o terceiro
compara a inclinação real da anca com a inclinação medida pelo inclinómetro.
A seta presente em todas experiências representa o ponto
onde o atraso entre a posição real e a posição esperada é maior.
Para o primeiro teste usou-se um tempo de movimento de 2s,
que representa o tempo que a perna demora a percorrer cada uma das arestas do
rectângulo. Os ganhos testados variaram entre 0.3 e 0.5 (Ilustração
3‑23 até Ilustração 3‑25).
No segundo teste usou-se como tempo de movimento 4s e
variou-se o ganho do controlador entre 0.1 e 0.5 (Ilustração
3‑26 até Ilustração 3‑30).
Por último, testou-se o mesmo movimento com um tempo de
execução de 5s por aresta (Ilustração
3‑31 até Ilustração 3‑32).
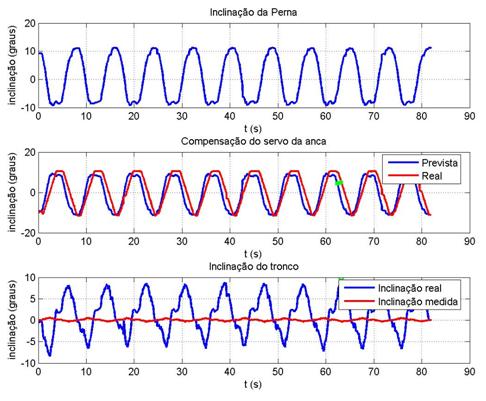
Ilustração 3‑23 - Teste inclinómetros t=2s k=0.3
Máximo tempo de atraso = 0.80s
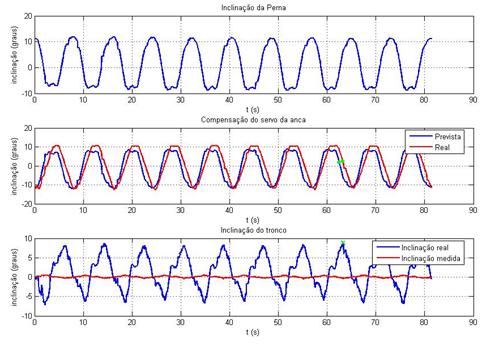
Ilustração 3‑24 - Teste inclinómetros t=2s k=0.4
Máximo tempo de atraso = 0.80s
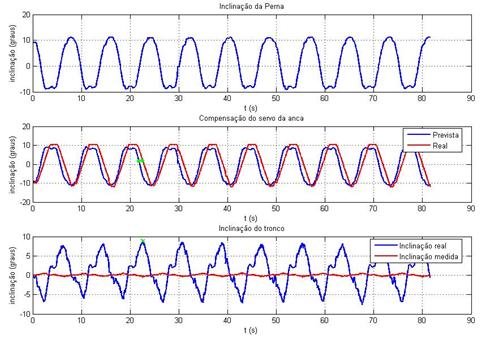
Ilustração 3‑25 - Teste inclinómetros t=2s k=0.5
Máximo tempo de atraso = 0.78s
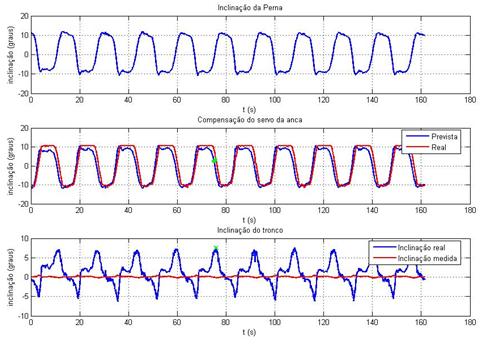
Ilustração 3‑26 - Teste inclinómetros t=4s k=0.1
Máximo tempo de atraso = 0.88s
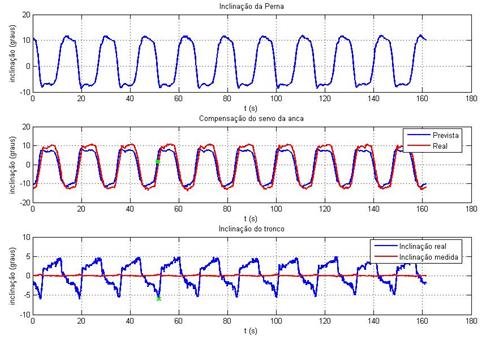
Ilustração 3‑27 - Teste inclinómetros t=4s k=0.2
Máximo tempo de atraso = 0.58s
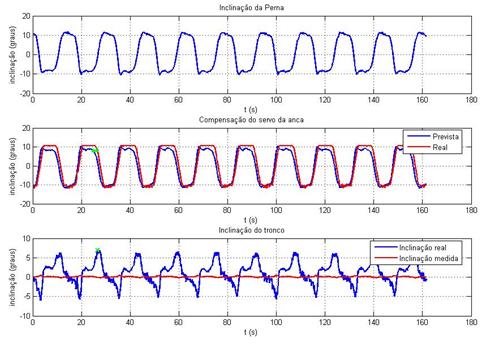
Ilustração 3‑28 - Teste inclinómetros t=4s k=0.3
Máximo tempo de atraso = 1.56s
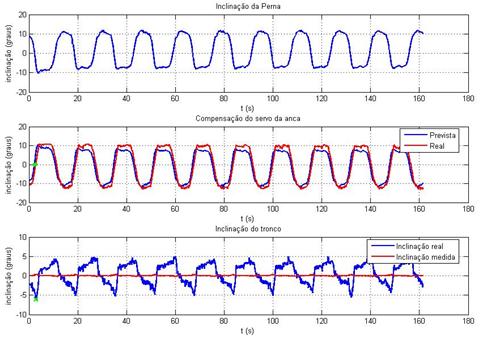
Ilustração 3‑29 - Teste inclinómetros t=4s k=0.4
Máximo tempo de atraso = 0.58s
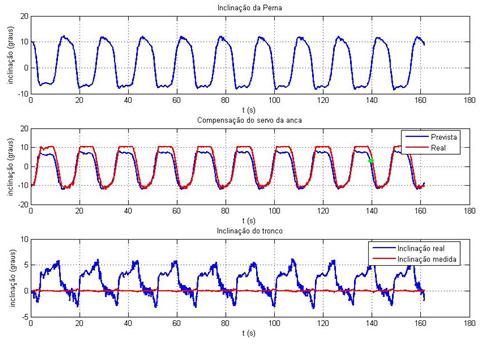
Ilustração 3‑30 - Teste inclinómetros t=4s k=0.5
Máximo tempo de atraso = 0.84s
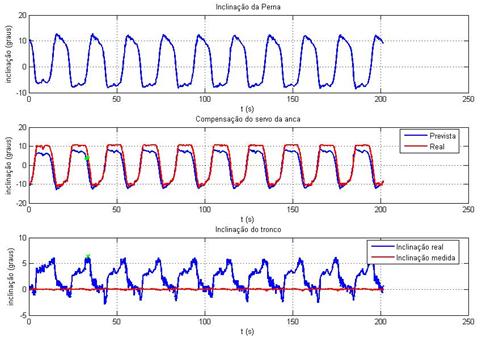
Ilustração 3‑31 - Teste inclinómetros t=5s k=0.3
Máximo tempo de atraso = 0.98s
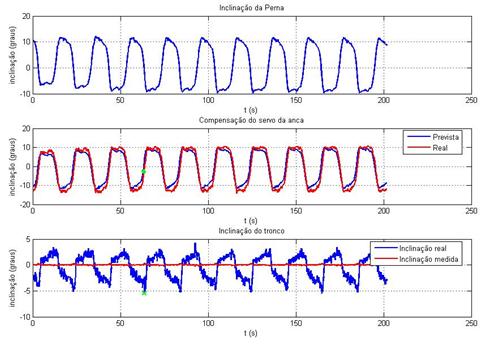
Ilustração 3‑32 - Teste inclinómetros t=5s k=0.5
Máximo tempo de atraso = 0.55s
O comportamento dos inclinómetros, de um modo geral e tendo
em conta a sua utilidade prática, é satisfatório, isto porque, dado que a parte
superior da estrutura têm pouca massa relativamente ao resto do corpo, o facto
de haver ligeiros atrasos na sua compensação não irá afectar de forma explicita
o CoP.
Analisando mais pormenorizadamente os resultados obtidos, verifica-se
a presença de um atraso sistemático na resposta do compensador. Este atraso
nunca será eliminado apenas poderá ser melhorado, isto dado que o compensador
actua em real-time, portanto, só se
se conseguisse prever o futuro é que se poderia anular o atraso.
Aumentar o ganho do compensador melhora a sua resposta mas o
aumento do ganho em excesso também causa invariavelmente oscilações. Foi para
evitar esta situação que se limitou logo à partida o ganho do controlador aos
valores entre 0.1 e 0.5, isto porque, abaixo do primeiro a compensação é muito
lenta, e acima dos 0.5 começa a haver oscilação.
A curva de resposta do controlador, apresentada na Ilustração
3‑21, favorece a ocorrência precoce de oscilações, já
que essa resposta não apresenta uma banda-morta em torno do zero. Alterando
este facto poder-se-á aumentar o ganho, melhorando ligeiramente a resposta do
controlador sem a ocorrência de oscilações mas ainda assim, a melhoria poderá
ser pouco significativa e permitirá a existência de um erro em torno de zero,
com metade da largura da banda-morta.
Outro dos factores que provoca atraso é o filtro passa baixo
(média pesada de duas amostras) aplicado às medidas do inclinómetro. Este
filtro é no entanto necessário para eliminar picos causados por ruído.
Uma das preocupações com os inclinómetros revelar-se-á
quando estes forem utilizados durante a execução de movimentos mais complexos, onde
as acelerações mecânicas do humanóide tenham uma dimensão apreciável pois
poderá acontecer nesses casos uma leitura errada da inclinação da anca. Será
necessário no futuro precaver este tipo de situações pois poderá ter
consequências nefastas uma compensação com base em valores adulterados.
Um movimento de alto-nível é uma actividade coordenada e
dividida em diferentes fases que no final perfazem uma acção, tal como um passo
ou um pontapé numa bola. Este tipo de algoritmos tem a difícil tarefa de coordenar
toda a estrutura de forma que o movimento seja realizado de forma coordenada e
garantindo sempre a estabilidade.
Para a compreensão do funcionamento destes movimentos são
necessários alguns conhecimentos, tal como o referencial usado para descrever o
movimento, os planos corporais e conhecimentos de planeamento de trajectórias. Os
planos usados no estudo do corpo humano são o plano sagital, que representa o plano
de simetria do ser humano, o plano frontal, que divide o corpo entre frente e
costas e o plano transversal que corta a parte de cima da parte de baixo do
corpo (Ilustração
4‑1). Também ilustrado estão os eixos de referência
usados e os sentidos arbitrados comos positivos. Nesse referencial o ponto
(0,0,0) corresponde à junção da primeira junta do pé direito com a placa do pé.
Outra das definições que vai ser falada é o centro de gravidade (CoG) e o
centro de pressão (CoP). O primeiro representa o ponto no espaço que reflecte a
distribuição das massas na estrutura humanóide. O segundo representa a
projecção no solo do centro de gravidade e permite concluir sobre a
estabilidade do movimento (numa situação de movimento quasi-estático). Na Ilustração
4‑2 está representado o CoG de cada um dos
componentes do robô humanóide com uma cruz, o círculo representa o CoG de toda
a estrutura e a sua projecção no solo.

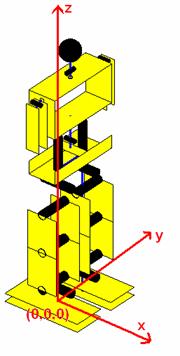
Ilustração 4‑1 - Planos corporais e eixos de referência
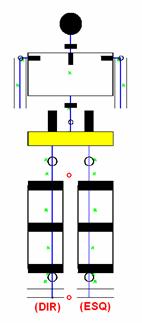
Ilustração 4‑2 -
Centro de Gravidade (CoG)
Os movimentos de alto-nível criados para o Robô Humanóide
foram desenvolvidos admitindo um movimento quasi-estático, quer isto dizer que
o movimento é executado a uma velocidade muito reduzida e, em cada fase do
movimento o centro de massa do robô está sobre o pé de suporte (no caso de só
um pé estar no solo), garantindo dessa forma que não haverá queda em qualquer
fase do movimento.
Em estruturas mecânicas constituídas por elos mecânicos
interligados por juntas articuladas, pode-se dividir a estrutura pelo número de
juntas e representar cada elo resultante por um referencial próprio. O robô
humanóide é um desses casos, em que toda a estrutura está dividida em 22 partes
unidas por 22 juntas. Como no entanto estes elos estão todos unidos, quando se
faz a atribuição de referenciais a cada um tem que se ter em conta a
dependência que existe entre esse elo e o anterior, há assim um conjunto de
elos unidos em série.
Há portanto, dois espaços de referência possíveis, um é o
espaço das juntas e representa a posição angular de cada junta e o outro é o
espaço cartesiano.
Para a delineação de trajectórias neste tipo de sistema há
dois tipos de planeamentos possíveis, ou no espaço cartesiano ou no espaço das
juntas. Há portanto, dois espaços variáveis, relacionáveis entre si.
Pode-se então questionar qual o melhor espaço de referência
para planear a trajectória? Na resposta a esta pergunta à que ter em
consideração alguns aspectos. A trajectória será sempre executada por juntas,
logo, apesar de haver uma relação directa entre espaço das juntas e espaço
cartesiano, um movimento definido no espaço cartesiano será descrito por uma
aproximação do movimento no espaço das juntas. Por outro lado, há certo tipo de
definições que têm de ser, obrigatoriamente, fornecidas no espaço cartesiano,
por exemplo, se se pretender subir escadas tem que se definir a altura da
escada como sendo a distância que o pé tem de se elevar para fazer o movimento.
A física responde a esta questão com a cinemática, que é uma
relação matemática que relaciona um movimento das juntas com o espaço
cartesiano e vice-versa. No primeiro a operação de transformação designa-se por
cinemática directa e quando a transformação é iniciada no espaço cartesiano e
remetida para o espaço das juntas há então uma operação de cinemática inversa.
Apesar de haver uma relação directa entre espaço das juntas
e espaço cartesiano, o mesmo não se verifica para o caso oposto, isto é, as
operações realizadas no espaço das juntas podem ser mapeadas no espaço
cartesiano sem qualquer tipo de ambiguidade, mas o contrário nem sempre se
verifica, Ilustração 4‑3. Para atingir o mesmo ponto cartesiano há duas
formas distintas tal como representado na figura seguinte.
Ilustração 4‑3 – Exemplo da redundância da cinemática
inversa
O conceito de cinemática directa já foi explicado, resta
agora saber como é que esta função funciona. Os elementos necessários para o
cálculo da cinemática directa são a posição das juntas e o comprimento dos
elos. O fundamento básico para o seu cálculo reside nas conhecidas funções da
trigonometria (sin, cos), que relacionam um ângulo, o cateto oposto, o cateto
adjacente e a hipotenusa. Considerando a nossa hipotenusa o comprimento do elo
e associando um referencial à junta de suporte ao elo, podemos reflectir a
posição cartesiana do outro extremo do elo no referencial criado. Pensando
agora que se tem ligado a esse extremo outra junta com outro elo, pode-se
efectuar o mesmo procedimento e saber o ponto do extremo da segunda junta e
assim sucessivamente até ao fim da cadeia.
O exemplo apresentado está representado no espaço
bidimensional mas o robô humanóide tem liberdade de movimentos no espaço
tridimensional o que complica um pouco mais as contas e tem também 22 juntas
com pontos de derivação (onde há duas juntas ligadas com direcções diferente). Estes
dois novos desafios encontrados podem ser ultrapassados utilizando técnicas
matriciais para resolução de cinemática directa. Convêm referir, antes de
passar à solução, que o problema da derivação pode ser visto como duas séries
de juntas distintas que partem do mesmo ponto, dividindo assim o problema em
dois.
Qualquer solução apresentada têm de começar por uma junta
primária, onde a cadeia começa, e, no caso do humanóide há várias
possibilidades, porque se têm vários pontos extremos que tanto pode ser o
início como o fim da cadeia (ex.: pé direito ou esquerdo, ou braço, ou cabeça).
A questão que aqui se coloca é qual é que deve ser o ponto de partida? A
resposta reside noutra pergunta, quem é que está a suportar a estrutura, ou
quem está assente na origem do referencial cartesiano (pressupondo que a origem
é o ponto de contacto do humanóide com o solo)? Dado que o humanóide ainda não
faz o pino, só há três hipóteses de suporte, ou pé direito, ou pé esquerdo, ou
os dois. Quando é um pé ou outro, o problema está resolvido, e quando são os
dois? Nesse caso pode-se optar por um qualquer e, garantidamente a solução será
a mesma.
Depois de todas as condições iniciais definidas está na
altura de apresentar a técnica usada no cálculo da cinemática directa, que é o
algoritmo de Denavit-Hartenberg.
Este algoritmo propõe a criação de uma matriz que contempla
todas as relações entre as juntas e efectua posteriormente uma multiplicação
iterativa desta matriz com uma matriz de transformação. Cada uma das matrizes
que resulta de cada iteração pode ser aplicada ao ponto que representa a
respectiva junta e o resultado é a posição cartesiana dessa junta. Mas essa
matriz não representa apenas a posição cartesiana da junta, ela também fornece
a orientação dessa junta, isso quer dizer, que se em vez de um ponto essa
matriz for aplicada a uma superfície representativa da junta, o resultado seria
a posição e orientação dessa junta.
A cinemática inversa determina os valores das juntas que se
adequam a uma dada configuração no espaço cartesiano. Este é um problema que
nem sempre tem uma solução analítica e pode também ter várias soluções, daí ser
muito mais complicada a cinemática inversa do que a directa.
Os métodos existentes para calcular a cinemática inversa
são:
 Transformações
inversas;
Transformações
inversas;
 Matrizes
duais;
Matrizes
duais;
 Métodos
iterativos;
Métodos
iterativos;
 Abordagens
geométricas.
Abordagens
geométricas.
O problema da cinemática inversa agrava-se com o número de
juntas, por isso, se se pensar que o robô humanóide tem 22 juntas parece haver
aqui um caso complicado. A solução para este problema assenta na divisão de
toda a estrutura e na criação de restrições ao cálculo da cinemática inversa.
Há assim uma fórmula de cálculo da cinemática inversa para o caso de 2 juntas,
que é:
Considerando l1 e l2 como os comprimentos dos elos das
juntas 1 e 2, respectivamente, e sendo x e y, o ponto cartesiano da extremidade
do segundo elo, então,
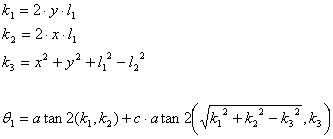
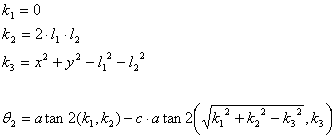
A variável c,
serve para eliminar a redundância relativa ao “cotovelo” da configuração. Tal
como mostrado na Ilustração 4‑3, o “cotovelo” entre os dois elos, pode ficar
virado para cima ou para baixo, dessa forma a variável c pode tomar valores de -1 ou 1, representando cada um deles uma
dessas situações.
Usando esta fórmula de cinemática 2R, pode-se aplicar ao
robô humanóide a duas juntas que se pretenda actuar e restringir o movimento de
outras juntas associadas de forma a perfazer a acção definida no espaço
cartesiano.
O movimento de marcha está dividido em três fases mais um
ponto intermédio. Para este movimento são definidos 4 parâmetros de referência:
 Sl
–
Comprimento do passo;
Sl
–
Comprimento do passo;
 Hh
– Altura da anca;
Hh
– Altura da anca;
 Yg
– Posição lateral do centro da anca;
Yg
– Posição lateral do centro da anca;
 Fc
– Máxima elevação do pé.
Fc
– Máxima elevação do pé.
Obviamente o comprimento do passo define a distância que o
pé livre têm de percorrer desde o início até ao fim do passo. A altura da anca
reflecte a flexão das pernas durante o movimento, isto é, determina que no
início do movimento, com o intuito de baixar o centro de gravidade, a anca deve
estar a determinada posição do solo. A posição lateral do centro da anca é
definida para se garantir que o centro de gravidade se encontra sobre o pé de
suporte, dessa forma e, por razões de simetria sagital da estrutura, o centro
da anca deverá estar aproximadamente coincidente com o centro do pé de suporte,
qualquer que ele seja. A máxima elevação do pé define o ponto intermédio por
onde o pé livre terá de passar. Este ponto é muito importante porque, como as
trajectórias são definidas no espaço das juntas, se só fosse enviado para as
SCU o valor das posições iniciais e finais do passo, iria ser calculada uma
trajectória em que o pé livre avançaria por baixo do solo (na realidade
cairia!).
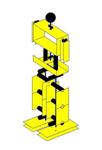
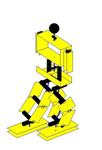
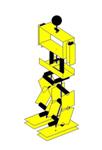
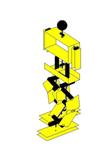
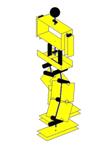
Ilustração 4‑4 - Sequência do movimento de marcha
Num primeiro momento o pé livre (assumindo que é o pé
esquerdo), recua metade do comprimento do passo e o CoG é colocado sobre a
parte de trás pé direito. Nesta mesma fase, o centro da anca é também
posicionado, segundo o eixo dos yy, sobre o pé de suporte e, segundo o eixo dos
x, recua ¼ do comprimento do passo. Este recuo serve para garantir que a anca
acompanha o movimento do pé livre durante o seu trajecto.
Como foi estipulado um ponto intermédio de passagem, nesta
fase é enviado para as slaves os
valores das juntas da posição intermédia calculada. Neste ponto o pé livre executa
meio passo para a frente, mas fica parado no ar a uma altura Fc.
Durante esta fase a anca também acompanha o movimento do pé.
No final desta fase o centro da anca encontra-se exactamente alinhado segundo o
eixo dos xx com o pé de suporte e a posição segundo o eixo dos yy não se
altera.
4.2.2.1 Fase 3: fim
do passo
Depois de estar no ponto intermédio o pé livre deve ser
enviado para a sua posição final, ou seja terá de percorrer o meio passo que
falta. No fim desta fase a anca avançou ¼ do passo segundo o eixo dos xx e a
posição em yy não se altera.
4.2.2.2 Fase 4: preparação
do próximo passo
Como durante todas estas fases a posição em yy do centro da
anca não de alterou é agora necessário passar essa posição para cima do novo pé
de suporte. Durante este movimento da anca em yy, há também um movimento desta,
correspondente a ¾ do passo segundo o eixo dos xx. Este último ajuste garante
que no início do próximo passo a anca parte exactamente do mesmo ponto com que
partiu para o primeiro passo, mas desta vez com o pé de suporte diferente, isto
porque há simetria segundo o plano sagital.
Como o passo é um movimento que apresenta simetria no plano
sagital e frontal, para cada fase do movimento, então, o algoritmo usado, utiliza
essa característica para adaptar cada fase do movimento já calculado no
primeiro passo, de forma, a aplicar esses valores às juntas correspondentes no
outro lado do plano sagital. O algoritmo usado é então o representado na Ilustração
4‑5.
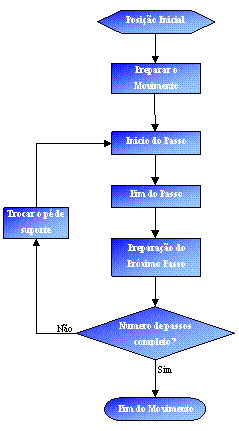

Ilustração 4‑5 - Algoritmo para a realização de vários
passos
O movimento de rotação possibilita ao robô humanóide mudar a
sua direcção, por isso é um movimento de enorme importância no desenvolvimento
de padrões de locomoção. Este movimento apresenta contudo uma dificuldade
intrínseca à própria concepção da estrutura, isto porque, apesar dos 22 graus
de liberdade existentes neste robô, não são comparáveis aos graus de liberdade
que um ser humano apresenta. Daí que para o ser humano este movimento de
rotação seja relativamente simples mas projectá-lo para este humanóide não seja
tão trivial assim.
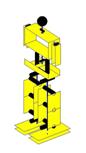
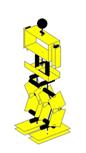
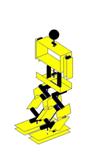
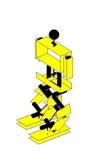
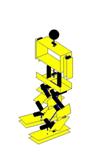
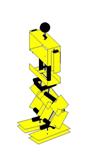
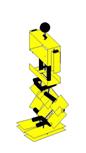
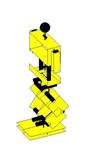
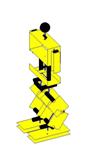
Ilustração 4‑6 - Fases do movimento de rotação
A sequência do movimento de rotação é bastante extensa, como
se pode ver pela Ilustração 4‑6. Este movimento está dividido em 8 fases. Esta
sequência poderá ainda ser encurtada com a junção de alguns movimentos, sem que
isso afecte a sua correcta execução.
Há vários parâmetros que definem este movimento, são eles:
 ang_iR – Inclinação das pernas que garante um CoG
assente no pé de suporte;
ang_iR – Inclinação das pernas que garante um CoG
assente no pé de suporte;
 ang_r
– Ângulo de rotação que se
pretende;
ang_r
– Ângulo de rotação que se
pretende;
 Hh
–
Altura da anca inicial desejada;
Hh
–
Altura da anca inicial desejada;
 Fc
–
Altura do pé durante o movimento de rotação.
Fc
–
Altura do pé durante o movimento de rotação.
O cálculo das fases é executado no espaço cartesiano e no
espaço das juntas. Este movimento pode ser explicado em quatro fases, estando as
várias fases reais encapsuladas em cada uma destas quatro. A primeira pode ser
designada por fase de preparação, é quando o humanóide usa os parâmetros Hh e ang_iR
para flectir as pernas e incliná-las de forma a alinhar o CoG com o pé de
suporte. A segunda fase envolve os passos de levantar, rodar e pousar e
representa o movimento de rotação do pé livre. Como terceira fase está o movimento
complicado de passar o CoG para o novo pé de suporte. Esta fase representa um
único movimento bastante complexo, que consiste num sincronismo de juntas
preciso, calculado através de cinemática inversa aplicada a ambas as pernas.
Como última fase designa-se o movimento de levantar o novo pé livre, rodá-lo e
voltar a pousá-lo no solo.
4.3.1.1 Fase 1: preparar
o movimento
Nesta fase ideológica estão representadas 2 fases reais do
movimento no robô humanóide. Portanto, há um primeiro momento em que as pernas
flectem ficando a altura da anca a Hh
metros do solo, Ilustração 4‑7. O valor de Hh
é definido a partir da percentagem da altura máxima da anca. Dessa forma, e
apesar deste valor poder ser alterado, ele está definido como sendo 95% da
altura máxima da anca.
Num segundo momento há uma inclinação lateral de ang_iR das pernas com o intuito de
colocar o centro de pressão sobre o pé de suporte.
4.3.1.2 Fase 2: levantar,
rodar e pousar
Esta fase representa 3 fases na prática e representa a
rotação do pé livre, tal como representado na Ilustração
4‑10. O pé livre efectua o movimento de rotação a uma
altura predefinida de Fc.
4.3.1.3 Fase 3:
transferir CoG para o novo pé de suporte
Este é o ponto mais delicado deste algoritmo. Como se vê
pela Ilustração
4‑11, para o pé rodar, têm que se rodar toda a perna
segundo uma circunferência. O eixo dessa circunferência provém da junta que
efectua o movimento de rotação. O problema deve-se ao desalinhamento que vai
ocorrer nos pés, segundo o plano frontal quando o pé livre roda. Como se pode
observar pela Ilustração 4‑13, há um desalinhamento entre as juntas
responsáveis por mover a anca no plano frontal.
Para passar o CoG para o novo pé de suporte vai ter que
haver um movimento de rotação da anca, articulado de forma perfeita entre as
duas pernas.
Ilustração 4‑13 - Desalinhamento das juntas que controlam o
movimento lateral da anca
4.3.1.4 Fase 4: acabar
movimento
A finalização do movimento corresponde às fases em que o
novo pé livre, se eleva, roda e pousa no solo, alinhado segundo o eixo dos yy,
com o pé de suporte.
Este é dos três, o movimento mais simples que está
implementado. A sua utilidade prática incide basicamente sobre as competições
de robôs humanóides que existem, em que um dos testes é o remate de uma bola.
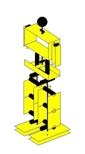
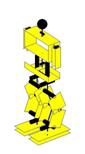
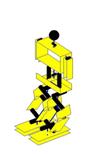
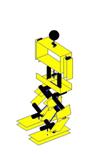
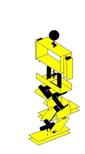
Ilustração 4‑14 - Sequência do movimento Pontapé
Os parâmetros que definem este movimento são os seguintes:
 ang_iR – Inclinação das pernas que garante um CoG assente
no pé de suporte;
ang_iR – Inclinação das pernas que garante um CoG assente
no pé de suporte;
 Hh
– Altura da anca inicial desejada;
Hh
– Altura da anca inicial desejada;
 Fc –
Altura do pé livre aquando do remate.
Fc –
Altura do pé livre aquando do remate.
Este movimento tem as mesmas características iniciais do
movimento de rotação, ou seja há uma fase de preparação onde as pernas são
flectidas e o CoG é transferido para o pé de suporte. Depois há uma fase de
elevação do pé livre a uma altura Fc
e seguidamente, o pé livre avança para frente no sentido de perfazer um remate.
A altura Fc é também o ponto segundo
o eixo dos zz em que o pé vai embater com a bola, por isso, ao contrário do que
se passa com o movimento de rotação esta altura têm que ser especificada tendo
em vista o ponto de impacto do remate.
O avanço final do pé livre é executado unicamente pela junta
do joelho. Este movimento consiste em inverter o ângulo que a junta tinha com a
vertical, Ilustração 4‑15 e Ilustração 4‑16.
O protocolo de comunicações entre o PC e o robô foi
desenvolvido em Matlab.
Dessa forma existe todo um conjunto de comandos que permite a
interacção com o robô. Devido à necessidade constante de enviar cadeias de
comandos de actuação e leitura, semelhantes entre si mas com parâmetros
diferentes, tornava-se necessário construir uma plataforma superior que
operasse esses comandos de uma forma autónoma e transparente para o utilizador.
Para satisfazer essa necessidade havia duas formas:
 Criar
funções Matlab que agregassem todas essas cadeias de comandos;
Criar
funções Matlab que agregassem todas essas cadeias de comandos;
 Criar
uma aplicação gráfica em que cada cadeia de comandos fosse representada por um
objecto.
Criar
uma aplicação gráfica em que cada cadeia de comandos fosse representada por um
objecto.
A primeira opção tem a desvantagem de ter de se criar
funções suficientes para albergar o leque de possibilidades existentes na
combinação dos comandos e o facto do utilizador ter de saber a finalidade de
cada uma dessas funções. A segunda opção apresenta-se como a melhor para a
finalidade requerida, mas tem a desvantagem de se despender muito tempo com
pormenores visuais ao invés de criar mais funções e mais robustas.
Foi nesse sentido que surgiu a ideia de criar um Graphical
User Interface (GUI) que agregasse num único pacote grande parte do trabalho
que já tinha sido desenvolvido anteriormente, entre os quais a comunicação com
o robô humanóide, os algoritmos de movimentos de alto nível, locomoção e
rotação e que mostrasse uma imagem virtual do que se estivesse a fazer.
O Matlab fornece uma ferramenta para desenvolvimento de
Graphical User Interface (GUI), que se chama GUIDE.
Ilustração 5‑1 - GUIDE
As razões para a escolha desta ferramenta de desenvolvimento
recaem sobre os seguintes pressupostos:
 O
protocolo de comunicações RS-232 estava desenvolvido em Matlab;
O
protocolo de comunicações RS-232 estava desenvolvido em Matlab;
 Muito
do trabalho desenvolvido para este projecto estava em Matlab, entre os quais os
algoritmos de movimentos, as definições e animações virtuais do Humanóide,
entre outros;
Muito
do trabalho desenvolvido para este projecto estava em Matlab, entre os quais os
algoritmos de movimentos, as definições e animações virtuais do Humanóide,
entre outros;
 Não
havia necessidade de aprender linguagens de alto-nível vocacionadas para o
desenvolvimento visual, como C#, Visual Basic, Java, etc.
Não
havia necessidade de aprender linguagens de alto-nível vocacionadas para o
desenvolvimento visual, como C#, Visual Basic, Java, etc.
O aspecto visual da ferramenta GUIDE está representado na
seguinte ilustração:
Ilustração 5‑2 - Workspace GUIDE
Uma das desvantagens desta ferramenta consiste no pequeno
leque de objectos de desenvolvimento mas é também este um dos factores que
torna o desenvolvimento da aplicação gráfica fácil porque não há muito por onde
escolher. Além dos objectos de desenvolvimento presentes na Ilustração
5‑2, é também possível desenvolver uma barra de menu,
ou menus de contexto, Ilustração
5‑3. Os menus de contexto são acedidos através do click com o botão direito do rato e os
seus dados e estrutura são dependentes da posição do rato nesse momento, daí o
nome “menu de contexto” porque depende da situação em que é chamado.
Cada um dos objectos de desenvolvimento tem um conjunto de
especificações que tem de ser definidas para a sua correcta utilização. Devido
à extensão destas especificações não é exequível inserir neste relatório todas
as suas definições mas remeto qualquer questão relacionada com alguma dessas
especificações para a ajuda do Matlab que durante o desenvolvimento de
aplicação se revelou imprescindível e muito bem organizada. É também de referir
que o Matlab disponibiliza vídeos tutoriais para a inicialização no
desenvolvimento de GUIs.
Ilustração 5‑3 - Criação de Menus
O ambiente de desenvolvimento GUIDE permite modelar o
aspecto visual da aplicação, mas não permite associar tarefas a objectos. Para
isso, juntamente com o ficheiro visual está um script que alberga todas as funções relativas aos objectos da
aplicação. Cada tipo de objecto tem um conjunto de chamadas ao sistema
diferentes, isto é, a função que é despoletada por uma acção. Por exemplo,
clicar com o botão esquerdo do rato ou com o botão direito, são acções
diferentes que podem encetar uma função diferente. Resumindo, há um script Matlab que alberga todas as
funções desencadeadas por uma qualquer acção executada sobre o GUI.
A estrutura do script,
inicia-se com código associado à iniciação e encerramento do GUI. Estas funções
iniciais não devem ser alteradas, pois definem parâmetros essenciais para a
execução do GUI. As funções que devem ser alteradas são os callbacks (chamadas ao sistema) que cada acção no GUI desencadeia.
Para isso, com o GUIDE aberto clica-se com o botão direito do rato sobre um
objecto e é mostrado um conjunto de callbacks
relativos a esse objecto. Ao escolher um desses callbacks vai acontecer um de dois cenários, se o callback já estiver presente no script então é mostrado esse trecho de
código já definido, se o callback não
estiver definido então aparece no script
o cabeçalho da função pronto a ser definido.
Sempre que se cria uma nova função de callback esta tem presente nos seus parâmetros de entrada uma
estrutura designada por handles e que
contêm o identificador de todos os objectos presentes no GUI. Através deste
identificador e dos comandos get e set, pode-se aceder ou re-definir,
respectivamente, parâmetros desse objecto.
 get(h,'PropertyName')
get(h,'PropertyName')
 set(h,'PropertyName',PropertyValue,...)
set(h,'PropertyName',PropertyValue,...)
O handles é uma
estrutura associada a uma figura, neste caso, essa figura é onde se apresenta o
GUI. Há um conjunto de comandos que permitem aceder e trabalhar com esta
estrutura, são eles:
 guidata
– permite guardar ou ler dados
associados a uma figura
guidata
– permite guardar ou ler dados
associados a uma figura
 getappdata
– obtêm todos os dados ligados a uma
figura
getappdata
– obtêm todos os dados ligados a uma
figura
 setappdata
– guarda os dados associados a uma
figura
setappdata
– guarda os dados associados a uma
figura
O comando guidata
usa internamente os outros comandos mencionados, mas enquanto os outros dois
comandos são usáveis com qualquer tipo de figura, o comando guidata é específico de GUI e é um
comando universal pois permite tanto a leitura da estrutura como a sua
salvaguarda na figura.
Está assim descrito o comando mais importante quando se cria
o script referente ao GUI, porque
este comando quando esquecido ou mal usado pode originar muitos problemas
difíceis de detectar. Um desses casos é quando se têm uma série de funções a serem
executadas em paralelo e todas a usar a estrutura universal em que só a última
a fazer a salvaguarda da estrutura na figura é que vai ser bem sucedida. Todas
as outras funções, apesar de terem feito a salvaguarda, vão ver os seus dados
reescritos pela última função a executar a salvaguarda (guidata).
As definições adoptadas para a construção do modelo
matemático e visual do Humanóide foram retiradas de medições reais e/ou de
medições efectuadas no modelo CATIA do robô Humanóide. Os dados a seguir
apresentados representam a informação usada para a modelação matemática do robô
humanóide usada no simulador. Estes dados não inviabilizam que no futuro se
tenha que proceder a novas medidas ou ajustes aos valores usados.
|
Elo
|
Comprimento (m)
|
|
Pé – tornozelo
|
0.0470
|
|
Tornozelo – tornozelo
|
0.0200
|
|
Tornozelo – joelho
|
0.0950
|
|
Joelho – anca
|
0.0950
|
|
Anca – anca
|
0.0555
|
|
Anca – anca
|
0.0360
|
|
Secção da anca (z)
|
0.0325
|
|
Secção da anca (y)
|
0.0840
|
|
Anca – tronco
|
0.0215
|
|
Elo
|
Comprimento (m)
|
|
Tronco – tronco
|
0.0380
|
|
Tronco – tronco
|
0.0230
|
|
Secção do tronco (z)
|
0.0860
|
|
Secção do tronco (y)
|
0.0120
|
|
Tronco – pescoço
|
0.0147
|
|
Pescoço – cabeça
|
0.0270
|
|
Tronco – ombro
|
0.0180
|
|
Ombro – pulso
|
0.1151
|
Tabela 5‑1 - Dimensões dos Elos
|
Componente
|
Massa (kg)
|
|
Pé
|
0.524
|
|
Tornozelo
|
0.165
|
|
Perna
|
0.410
|
|
Coxa
|
0.371
|
|
Anca baixa
|
0.239
|
|
Anca cima
|
0.274
|
|
Componente
|
Massa (kg)
|
|
Secção da
anca
|
1.212
|
|
Cintura
|
0.246
|
|
Secção do
tronco
|
0.457
|
|
Pescoço/Cabeça
|
0.067
|
|
Ombro
|
0.071
|
|
Braço
|
0.064
|
Tabela 5‑2 - Massa dos Componentes
Os centros de massa foram medidos recorrendo à ferramenta de
modelação CATIA. Para isso, criou-se um referencial no canto superior direito
do pé direito, com o eixo dos xx perpendicular ao plano sagital, o eixo dos yy
perpendicular ao plano lateral e o eixo dos zz perpendicular ao plano transversal.
Como a estrutura apresenta simetria em relação ao plano
sagital, criando um referencial simétrico no pé esquerdo obtém-se para o lado
esquerdo da estrutura os mesmos valores para o centro de massa dos componentes
do lado esquerdo. Por essa razão só são apresentados na tabela os centros de
massa relativos ao referencial do pé direito.
|
Componente
|
Centro de Massa (mm)
|
|
xx
|
yy
|
zz
|
|
Pé direito
|
40
|
142
|
17
|
|
Tornozelo
direito
|
45
|
107
|
34,2
|
|
Perna
direita
|
46,3
|
102
|
94,5
|
|
Coxa direita
|
41
|
103,3
|
180,7
|
|
Anca direita
1
|
42,8
|
103,7
|
264,3
|
|
Anca direita
2
|
40,5
|
115,5
|
295,8
|
|
Ombro
direito
|
-12,24
|
109,47
|
524,2
|
|
Braço
direito
|
-24,18
|
101,12
|
467
|
|
Barra anca
|
95,9
|
118,4
|
358,9
|
|
Cintura
|
93,9
|
114
|
413,4
|
|
Tronco
|
95,3
|
111,8
|
494,8
|
|
Pescoço
|
95,3
|
121,3
|
554,6
|
Tabela 5‑3 - Centros de Massa dos Componentes
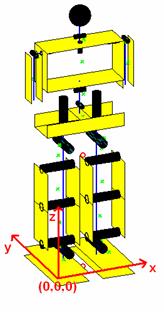
Ilustração 5‑4 - Centros de Massa com o referencial
utilizado
A relação de transmissão existente entre os servos e as
juntas apresentam valores de 1, 2.5 ou 3.75, esses valores estão representados
na Tabela 5‑4. A numeração das juntas está representada na Ilustração
5‑5.
|
Junta
|
Relação de
Transmissão
|
|
Junta
1
|
2.5
|
|
Junta
2
|
2.5
|
|
Junta
3
|
2.5
|
|
Junta
4
|
2.5
|
|
Junta
5
|
3.75
|
|
Junta
6
|
1
|
|
Junta
7
|
1
|
|
Junta
8
|
3.75
|
|
Junta
9
|
2.5
|
|
Junta
10
|
2.5
|
|
Junta
|
Relação de
Transmissão
|
|
Junta
11
|
2.5
|
|
Junta
12
|
2.5
|
|
Junta
13
|
1
|
|
Junta
14
|
1
|
|
Junta
15
|
1
|
|
Junta
16
|
1
|
|
Junta
17
|
1
|
|
Junta
18
|
1
|
|
Junta
19
|
1
|
|
Junta
20
|
1
|
Tabela 5‑4 -
Relação de transmissão das juntas
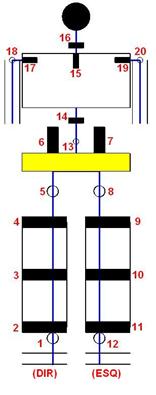
Ilustração 5‑5 - Número de cada junta no simulador
Nesta secção pretende-se analisar e explicar a organização
do GUI. Primeiramente são analisados os componentes que compõem a aplicação,
depois é abordada a forma como o código está organizado e só no fim se fará uma
pequena descrição dos ficheiros utilizados por toda a aplicação.
Não se pretende explorar detalhes de código mas sim dar uma
panorâmica geral de como tudo encaixa e funciona.
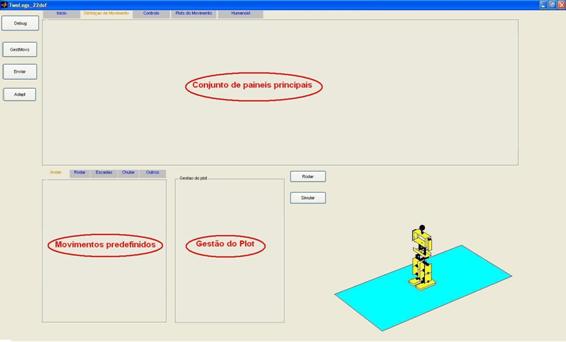
Ilustração 5‑6 - Divisão do GUI
O GUI TwoLegs_22dof está dividido em três áreas:
 Conjunto
paineis de principais
Conjunto
paineis de principais
 Movimentos
Predefinidos
Movimentos
Predefinidos
 Gestão
do Plot
Gestão
do Plot
 Botões
vários
Botões
vários
Cada uma destas áreas está subdividida em partições mais
pequenas que serão analisadas nas secções seguintes.
5.3.1.1 Conjunto de
painéis principais
Nesta área do GUI estão incluídas as funcionalidades de
actuação directa com o Humanóide, daqui podem distinguir-se os painéis:
 Inicio
Inicio
 Definição
do Movimento
Definição
do Movimento
 Controlo
Controlo
 Plots
do Movimento
Plots
do Movimento
 Humanóide
Humanóide
Ä Inicio
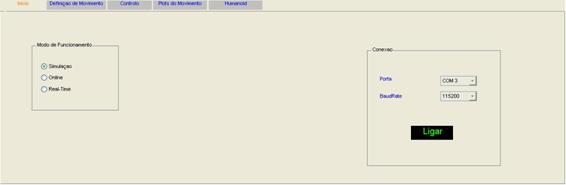
Ilustração 5‑7 - Aspecto visual do painel inicio
Este painel ainda não está completamente desenvolvido. A
ideia presente é que nele sejam incluídas as definições de funcionamento da aplicação,
como o modo de funcionamento, as definições de comunicações, gestão de
movimentos guardados e outras funcionalidades que de alguma forma interfiram
com o funcionamento global da aplicação. Até este momento só as definições de
comunicação estão definidas e operacionais, tudo o resto terá que ser
projectado visualmente e definido funcionalmente.
Ao nível das comunicações, pode-se definir a porta série que
está ligada ao master e o baudrate
usado, que corresponde a 115200bps. Quando se pressiona o “Ligar” é efectuada a
ligação ao master, activados os PWM, e feita uma leitura sensorial inicial para
actualização da base de dados interna da aplicação. Se todas as operações
anteriores forem bem sucedidas então o botão “Ligar” altera a sua string para “Desligar”.
Ä Definição
de Movimento
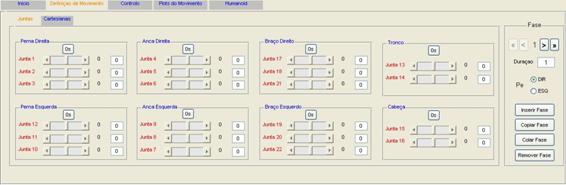
Ilustração 5‑8 - Aspecto visual do painel Definição de
Movimentos
Este painel permite ao utilizador efectuar um movimento do
humanóide. Essa definição de movimento, tal como está actualmente a aplicação
só permite que seja executado no espaço das juntas, apesar do painel que
permitirá definir o movimento no espaço cartesiano já esteja integrado nesta
secção.
Na Ilustração
5‑8 pode-se observar que os 22 DoF (graus de
liberdade) estão agrupados em 8 compartimentos, isto é uma referência directa à
arquitectura estrutural do sistema que tem 8 SCU, em que cada uma delas
controla 2 a
3 servomotores. A numeração das juntas corresponde ao descrito na Ilustração
5‑5. Cada slide
permite variar a junta entre -90 e 90 graus, o valor da junta é mostrado na text_box que segue o slide. Há outro elemento presente no
compartimento associado a cada junta, é uma dialog_box
que serve para ligar o movimento de uma junta a outra, isto é, se aplicar uma
posição a uma junta, essa posição é automaticamente aplicada à junta associada.
Esta associação pode ser feita ao inserir na dialog_box da junta dependente o valor da junta tutora, por
exemplo, se colocar na dialog_box da
junta 10 o valor 1, quer dizer que sempre que a junta 1 se mover a junta 10
também se moverá para a mesma posição mas o contrário já não se verifica. Outra
das particularidades desta função é a possibilidade de uma junta realizar o
movimento simétrico ao da junta tutora, para isso basta incluir um sinal “-“
antes do valor da junta tutora.
Pode também observar-se a existência de um painel com a
designação de “Fase”. Quando se define um movimento articulado, ele está
dividido em fases, em que cada uma delas descreve a sua duração e o pé de
suporte, é para isso que este painel existe. Sempre que se adiciona uma nova
fase ou um novo movimento predefinido, o painel da fase é actualizado.
Um pormenor usado na estruturação deste painel é a
existência de menus de contexto, Ilustração
5‑9, que permitem efectuar um conjunto de operações
básicas, tais como:
 Copiar/colar
– permite copiar o conjunto de valores das 3 juntas;
Copiar/colar
– permite copiar o conjunto de valores das 3 juntas;
 Inserir
– serve para colocar na fase actual as posições das 3 juntas que se pertencem a
outra fase anterior ou posterior;
Inserir
– serve para colocar na fase actual as posições das 3 juntas que se pertencem a
outra fase anterior ou posterior;
 Inverter
– realiza a inversão dos valores presentes nas 3 juntas;
Inverter
– realiza a inversão dos valores presentes nas 3 juntas;
 Espelho
vertical – troca os valores das juntas, isto é o valor da primeira passa para a
terceira e vice-versa.
Espelho
vertical – troca os valores das juntas, isto é o valor da primeira passa para a
terceira e vice-versa.
Ilustração 5‑9 - Menu de contexto para as juntas
Ä Controlo
Esta secção da aplicação não está desenvolvida, nem
visualmente, nem funcionalmente. O que se pretende que venha a ser inserido
neste painel é um conjunto de ferramentas que possibilite a actualização
dinâmica dos parâmetros do controlador PID. A forma como esses parâmetros serão
calculados não está de todo pensada, devido à dificuldade que o problema
envolve. Mas enquanto não se consegue uma solução para esse problema pode
simplesmente colocar neste painel uma ferramenta que possibilite o envio manual
dos parâmetros PID para cada um dos servos em cada fase do movimento.
Ä Plots
do Movimento
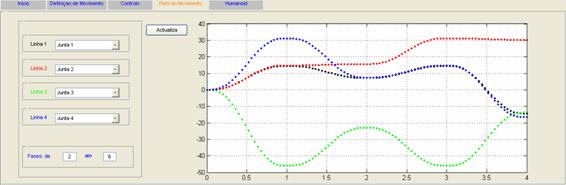
Ilustração 5‑10 - Aspecto visual do painel Plots do
Movimentos
Na definição do movimento o que a aplicação faz é a descrição
das posições das juntas em determinado instante, todo o cálculo da trajectória
que as juntas vão percorrer para atingir essas posições é efectuada nas SCU,
quando essas posições forem enviadas. Nesta secção da aplicação será possível
observar a trajectória que a slave
vai calcular para a execução do movimento. Neste painel podem-se definir até
quatro juntas para se visualizar o seu percurso e define-se também o intervalo
em que se pretende observar essa trajectória.
Uma das possíveis melhorias que poderá ser efectuada no
futuro é incluir também a visualização da trajectória no espaço cartesiano,
assim como a variação do centro de gravidade ao longo do movimento.
Ä Humanóide
Ilustração 5‑11 - Aspecto visual do painel Humanóide
O painel humanóide é onde são exibidas todas as leituras
feitas do robô. Actualmente só são actualizadas as leituras de posição dos
servomotores mas no futuro além destes valores também poderá ser incluído nesta
secção as leituras de outros parâmetros dos servos, tais como a velocidade e a
corrente, assim como as leituras dos sensores especiais, sensores de força e
inclinómetros.
5.3.1.2 Movimentos Predefinidos




Ilustração 5‑12 – Conjunto de painéis de Movimentos Predefinidos:
Andar, Rodar, Subir Escadas, Chutar e Outros
Na área dos movimentos predefinidos estão definidos os
movimentos de locomoção, rotação e pontapé na bola, assim como movimentos mais
básicos com baixar a anca ou inclinar as pernas, definidos no painel “Outros”. Cada
um destes movimentos tem as suas especificidades próprias, daí que todos estes
painéis apresentem campos diferentes.
Além dos movimentos já definidos, também está colocado um
painel para o movimento de subir escadas mas este algoritmo ainda não está
desenvolvido.
O painel com a designação de “Outros” ainda não está
completo, espera-se que sejam criados vários pequenos movimentos, há semelhança
dos movimentos já definidos.
5.3.1.3 Gestão do Plot


Ilustração 5‑13 - Gestão do Plot
Nesta secção do GUI pode-se ajustar as definições da
visualização do humanóide. È nesta zona que se define o que é que se pretende
ver, designadamente o tapete, a bola, as escadas e o centro de massa do
humanóide. Além de se definir o que se pretende ver na simulação também se pode
definir a posição e algumas especificações de cada um deste componentes, para
isso existem sub-paineis para cada um destes objectos. Essas definições são
basicamente a posição e as dimensões de cada um desses componentes.
Este painel tem também associado um menu de contexto que
permite alterar a perspectiva de visualização do robô humanóide virtual. A
localização deste menu nesta secção e não no próprio axis de simulação deveu-se a problemas de realização do mesmo
Para a organização dos dados necessários para o
funcionamento da aplicação criaram-se 7 estruturas afectas a diferentes áreas
do GUI. Cada uma dessas estruturas tem uma ligação directa aos diferentes
painéis existentes na aplicação. Essas estruturas são:
 DM
– Definição do Movimento;
DM
– Definição do Movimento;
 ME
– Movimentos especiais;
ME
– Movimentos especiais;
 PM
– Plot dos Movimentos;
PM
– Plot dos Movimentos;
 Ctrl
– Controlo;
Ctrl
– Controlo;
 Painéis;
Painéis;
 GP
– Gestão do Plot;
GP
– Gestão do Plot;
 JI
– Janela Inicial.
JI
– Janela Inicial.
Estas estruturas estão definidas e guardadas no interior da
estrutura da aplicação handles. À
excepção da estrutura de controlo que não está desenvolvida todas as outras têm
funções e aplicação real no GUI, por isso, serão definidas com mais detalhe.
5.3.2.1 DM -
Definição de Movimento
Nesta estrutura estão definidos os parâmetros associados ao
movimento, tais como posição das juntas e dimensões dos elos. Os campos
envolvidos nesta estrutura são:
 O
– Matriz com as distâncias e tamanhos das chapas que compões o robô virtual;
O
– Matriz com as distâncias e tamanhos das chapas que compões o robô virtual;
 L
– Array com os comprimentos de cada um dos elos do robô humanóide;
L
– Array com os comprimentos de cada um dos elos do robô humanóide;
 M
– Array com as massas dos componentes do humanóide;
M
– Array com as massas dos componentes do humanóide;
 q
– Matriz com as posições das 22 juntas nas fases do movimento;
q
– Matriz com as posições das 22 juntas nas fases do movimento;
 XYZRef
– Matriz com a posição do pé de suporte nas fases do movimento;
XYZRef
– Matriz com a posição do pé de suporte nas fases do movimento;
 fase
– Valor da fase actualmente em apresentação;
fase
– Valor da fase actualmente em apresentação;
 duracao
– Array com a duração de cada fase do movimento
duracao
– Array com a duração de cada fase do movimento
 tetaPe
– Array com a obliquidade do pé de suporte em relação ao eixo dos xx, em cada
fase;
tetaPe
– Array com a obliquidade do pé de suporte em relação ao eixo dos xx, em cada
fase;
 dependência
– Matriz de [22x22] que indica que juntas é que dependem de determinada junta.
dependência
– Matriz de [22x22] que indica que juntas é que dependem de determinada junta.
Nos campos envolvidos na estrutura DM além das definições de comprimentos e massas, têm-se alguns
campos que necessitam de uma explicação mais profunda.
O campo q é uma
matriz cujo número de linhas é igual ao número de fases total do movimento e o
número de colunas corresponde ao número de juntas existentes. Assim, fazendo o
cruzamento da fase, com o número da junta e obtêm-se a posição da junta
pretendida na fase em análise.
O campo XYZRef, da
mesma forma que o campo anterior disponibiliza nas linhas a fase e nas colunas as
coordenadas cartesianas (xyz), que indicam a posição do pé de suporte em cada
fase.
O campo tetaPe,
possibilita que o humanóide possa rodar livremente no espaço virtual, isto
porque é este campo que define a orientação do pé de suporte em cada uma das
fases.
A matriz de dependências existe com 22 linhas por 22 colunas
para facilitar as funções que a chamam. Nesta matriz, cada linha corresponde à
junta tutora e cada coluna a junta dependente, a intersecção entre estes dois
eixos pode estar a -1, 0 ou 1. Quando o valor é negativo quer dizer que a
dependência é invertida, isto é, se a junta tutora vai para a posição +20º,
então a junta dependente irá para a posição -20, quando o valor é zero é porque
não há dependência e quando é 1
a dependência é directa.
5.3.2.2 ME –
Movimentos especiais
A estrutura “Movimentos Especiais” contém as definições de
cada um dos movimentos predefinidos, tais como a locomoção e rotação. Esta
estrutura subdivide-se em sub-estruturas, que são:
 andar;
andar;
 rodar;
rodar;
 chutar;
chutar;
Cada uma destas sub-estruturas contém os parâmetros que são
passados nos painéis dos Movimentos Predefinidos.
5.3.2.3 Plot dos
Movimentos
Esta estrutura contém informação para a gestão do painel com
o mesmo nome. Assim tem-se nesta estrutura os campos:
 fase
– array de dois valores que define a fase inicial e final para mostragem;
fase
– array de dois valores que define a fase inicial e final para mostragem;
 L1
– Valor da junta referenciada pela linha 1;
L1
– Valor da junta referenciada pela linha 1;
 L2
– Valor da junta referenciada pela linha 2;
L2
– Valor da junta referenciada pela linha 2;
 L3
– Valor da junta referenciada pela linha 3;
L3
– Valor da junta referenciada pela linha 3;
 L4
– Valor da junta referenciada pela linha 4;
L4
– Valor da junta referenciada pela linha 4;
5.3.2.4 Paineis
Esta estrutura foi criada para compensar a falta de
elementos TabFolders de criação gráfica
no GUI no Matlab. Estes elementos possibilitam a troca do painel que está a ser
apresentado ao utilizador, através de etiquetas. Como há muita informação que
pode ser mostrada ao utilizador este tipo de elementos revela-se praticamente
essencial, por isso, a forma de contornar o problema foi criar TextBox, que são
as etiquetas e associar a cada uma delas um painel. Esta estrutura faz isso
mesmo, contêm a ligação entre TextBox e painel.
Os campos inseridos nesta estrutura correspondem as secções
do GUI que necessitam de TabFolder e são os seguintes:
 principal
– corresponde ao conjunto de painéis principais;
principal
– corresponde ao conjunto de painéis principais;
 DM
– faz a divisão entre juntas e cartesianas no painel Definição de Movimentos;
DM
– faz a divisão entre juntas e cartesianas no painel Definição de Movimentos;
 ME
– corresponde ao conjunto de painéis dos Movimentos Predefinidos
ME
– corresponde ao conjunto de painéis dos Movimentos Predefinidos
 GP–
corresponde ao conjunto de painéis da Gestão do Plot
GP–
corresponde ao conjunto de painéis da Gestão do Plot
5.3.2.5 Gestão do
Plot
Esta estrutura serve de suporte a toda a informação que se
encontra no plot do robô humanóide virtual. São aqui definidas todas as
posições cartesianas e dimensões de todos os componentes do plot, bem como
todas as etiquetas que referenciam esses mesmos componentes. Para isso esta
estrutura está dividida nos seguintes campos:
 def
– estrutura com as posições cartesianas e dimensões de todos os componentes do
robô humanóide;
def
– estrutura com as posições cartesianas e dimensões de todos os componentes do
robô humanóide;
 tapete
– definição do comprimento e posição do tapete onde está o robô humanóide;
tapete
– definição do comprimento e posição do tapete onde está o robô humanóide;
 escadas
– definição do número de escadas, do comprimento e altura dos degraus e da
posição em que se encontram;
escadas
– definição do número de escadas, do comprimento e altura dos degraus e da
posição em que se encontram;
 bola
– definição das dimensões e posição da bola;
bola
– definição das dimensões e posição da bola;
 COG_0
– definição do centro de gravidade de todos os componentes do robô quando este
está completamente na vertical;
COG_0
– definição do centro de gravidade de todos os componentes do robô quando este
está completamente na vertical;
 obj
– etiquetas para cada um dos objectos presentes no plot.
obj
– etiquetas para cada um dos objectos presentes no plot.
5.3.2.6 Janela
Inicial
Esta estrutura ainda não está completamente definida porque
ela corresponde ao painel designado por “início”, que também ainda não está
desenvolvido. Aqui devem ser colocados todos os campos relativos aos modos de
funcionamento da aplicação. A estrutura define actualmente a comunicação RS-232
e também a variável que contêm todos os dados de actuação relativos ao robô
real.
5.3.2.7 Botões
vários
A aplicação dispõe de um conjunto de botões “perdidos” que
se encontram no seio da aplicação. A utilidade destes botões não é definitiva e
a sua disposição na aplicação é para ser alterada numa versão futura.
Primeiramente, no canto superior esquerdo podem-se enumerar
3 botões tal como observado na Ilustração
5‑6:
 Debug
– permite o acesso à linha de
comandos e à variável handles;
Debug
– permite o acesso à linha de
comandos e à variável handles;
 GestMovs
– chama o GUI de gestão de ficheiros com
movimentos;
GestMovs
– chama o GUI de gestão de ficheiros com
movimentos;
 Enviar
– permite enviar para o MCU a
posição actualmente simulada;
Enviar
– permite enviar para o MCU a
posição actualmente simulada;
 Adapt
– permite definir a zero a actual
posição real do robô humanóide
Adapt
– permite definir a zero a actual
posição real do robô humanóide
A natureza completamente distinta das funções destes botões
perfaz a ideia de que a disposição destes elementos na aplicação não é a mais
adequada.
A outra secção de botões está associada ao axis principal (onde é simulado o
humanóide), neste ponto encontram-se dois botões:
 Rodar
– Permite alterar a perspectiva da visualização;
Rodar
– Permite alterar a perspectiva da visualização;
 Simular
– Executa um movimento planeado de todas as fases desenvolvidas.
Simular
– Executa um movimento planeado de todas as fases desenvolvidas.
Este último grupo de botões deveria estar representado numa
barra de ferramentas sobre o axis de
simulação. Juntamente com eles deveriam também ser agrupados botões de zoom ou pan, entre outras funções que se ache útil para uma animação mais
versátil. A sua inclusão numa barra de ferramentas desse género não foi possível
dado o Matlab não permitir associar barras a elementos tipo axis mas sim a figuras como um todo.
O código referente ao GUI está organizado segundo secções.
Cada secção tem uma função de inicialização de variáveis e de objectos além de
todas as funções de callback e funções auxiliares dos callbacks. As secções são
por isso divididas em sub-secções e estas podem também ter funções de
inicialização que são chamadas pela função de inicialização da secção
correspondente. Pretende-se com isso criar um efeito em árvore ramificada
unidireccional quando se inicia a aplicação, tal como representado no seguinte
organograma.
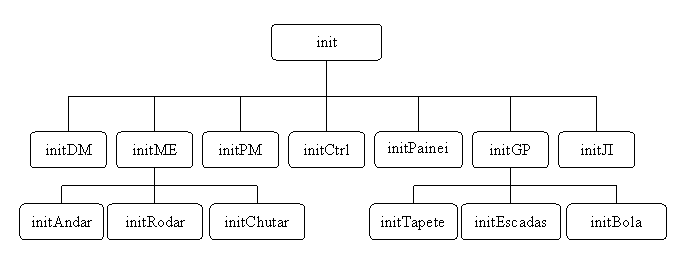

Ilustração 5‑14 - Inicialização do GUI
A divisão do m-file relativo ao GUI está por isso decomposta
nas seguintes secções e subsecções:
 Inicio
Inicio
 Janela
Inicial
Janela
Inicial
o
Inicialização
o
Comunicações
 Painéis
Painéis
o
Inicialização
o
Funções
 Definição
de Movimento
Definição
de Movimento
o
Inicialização
o
Menus de contexto
o
Espaço das juntas
o
Espaço cartesiano
o
Controlo de fase
 Movimentos
Especiais
Movimentos
Especiais
o
Inicialização
o
Outros
o
Chutar
o
Rodar
o
Andar
 Controlo
Controlo
o
Inicialização
 Plots
do Movimento
Plots
do Movimento
o
Inicialização
o
Funções
 Gestão
do Plot
Gestão
do Plot
o
Inicialização
o
Plot
o
Tapete
o
Escadas
o
Bola
o
Barra de ferramentas do Plot
o
Menus de contexto
 Outros
Outros
o
Debug
o
Gestor de Movimentos
Um dos objectivos para o desenvolvimento desta aplicação era
a pretensão de agrupar todo um conjunto de pequenas ferramentas que já tinham
sido desenvolvidas. Dessa forma, juntamente com o script principal do GUI tem-se também um conjunto de scripts que executam tarefas
independentes, tais como, cálculo da cinemática directa ou inversa. A descrição
de cada um deles é feita com mais detalhe abaixo, para uma análise mais
superficial está elaborada a Tabela 5‑6 para consulta rápida.
5.3.4.1 CinDir20dof.m
Este ficheiro define a função:
A = CinDir20dof( DM )
Esta função recebe como entrada uma estrutura do tipo
“Definição de Movimento” e devolve para a saída um array de matrizes de
transformação que se aplicam a cada um dos 20 graus de liberdade do robô
humanóide.
5.3.4.2 CoordJuntas
Este script
alberga a função:
handles = CoordJuntas( Ai,DM,handles )
Esta função efectua o cálculo da posição e orientação de
cada um dos objectos que compõe a estrutura virtual do robô humanóide. Como
parâmetros de entrada é dado o array de matrizes de transformação calculado
pela função CinDir20dof, como segundo parâmetro é fornecida a estrutura do tipo
“Definição de Movimentos” e o terceiro parâmetro é uma estrutura do tipo
“Definição de Objectos”, esta é também a estrutura de saída.
5.3.4.3 CinInv2R
Este script contém
a função:
[ang1,ang2] = CinInv2R( Pf,L,Signum )
Esta função faz o cálculo da cinemática inversa para 2 graus
de liberdade. Tem-se então como parâmetros de entrada o Pf, que é um vector com a posição cartesiana do ponto que se
pretende atingir, o L é um array com
os comprimentos dos elos e o Signum
resolve a redundância característica da cinemática inversa, ou seja, este valor
pode ser 1 ou -1 e define a orientação do “cotovelo”.
5.3.4.4 data_struct
A função definida por este ficheiro é:
robo = data_struct()
Esta função devolve uma estrutura com todos os parâmetros do
robô humanóide. Esta função está dividida em sub-estruturas em que além das
dimensões de alguns dos componentes do robô também existe um array de 8
estruturas que alberga as definições características de cada slave e de cada servo. A estrutura de
saída está ilustrada na Ilustração
5‑15.
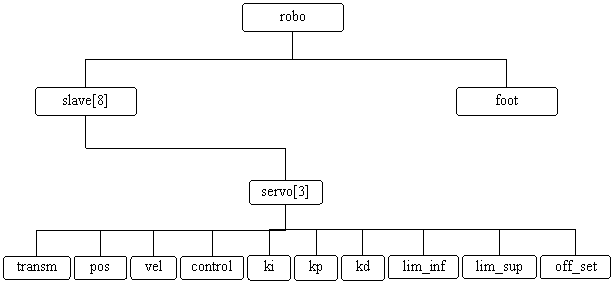

Ilustração 5‑15 - Organograma ilustrativo da estrutura robo
Dentro da estrutura “foot” estão algumas definições sobre as
dimensões e características deste componente. Há 8 estruturas do tipo “slave”,
cada uma alberga até 3 estruturas do tipo “servo” que contêm algumas das
definições associadas a cada um dos servos constituintes do robô humanóide.
Algumas das definições não são perceptíveis à primeira vista, por isso a seguir
é dada uma breve descrição de cada uma delas:
 transm
– relação de transmissão do servo;
transm
– relação de transmissão do servo;
 pos
– valor de posição actual do
servo;
pos
– valor de posição actual do
servo;
 vel
– valor do tempo de execução de
um movimento;
vel
– valor do tempo de execução de
um movimento;
 control
– tipo de controlo actualmente em
execução no servo;
control
– tipo de controlo actualmente em
execução no servo;
 ki,
kp, kd – parâmetros do controlador PID
quando activo;
ki,
kp, kd – parâmetros do controlador PID
quando activo;
 lim_inf
– limitação inferior do servo,
contando também com a limitação que a própria estrutura humanóide impõe ao
servo;
lim_inf
– limitação inferior do servo,
contando também com a limitação que a própria estrutura humanóide impõe ao
servo;
 lim_sup
– igual ao lim_inf mas para limitação
superior;
lim_sup
– igual ao lim_inf mas para limitação
superior;
 off_set
– o off_set de correcção (em relação
à posição vertical do robô).
off_set
– o off_set de correcção (em relação
à posição vertical do robô).
Esta estrutura que a função data_struct devolve ainda não está a ser totalmente aplicada. Esta
estrutura deverá ser a base de dados actualizada de tudo o que se passa com o
robô humanóide real.
5.3.4.5 DefineRob
Este script define
a função:
handles = DefineRob()
Esta função todas as dimensões dos elos e componentes do
robô humanóide. São definidos por esta função os comprimentos e massas dos
elos, bem como as distâncias e dimensões de cada uma das chapas que constituem
a estrutura. Todos estes dados são usados para o cálculo do CoG e para o plot do robô virtual.
5.3.4.6 DesenharRoboPZ
A função associada a este script é:
handles = DesenharRoboPZ( GP, axis_h )
O objectivo desta função é criar o primeiro plot do robô humanóide, para isso é-lhe
fornecido como parâmetros de entrada uma estrutura do tipo “Gestão do Plot”,
estrutura essa que alberga uma sub-estrutura denominada def e que é do tipo “Definição de Objectos”. Esta sub-estrutura é a
que a função CoordJuntas devolve e onde estão definidos
todos os objectos correctamente orientados e que compõe o robô humanóide. Outro
dos parâmetros que é fornecido a esta função é o axis_h, este parâmetro contêm o valor do handler corresponde ao axis
onde o plot será efectuado.
Na saída desta função está um array estruturado com a
etiqueta de cada um dos objectos desenhados. Este array é de extrema
importância, porque garante que qualquer alteração que tenha de ser feita a
qualquer um dos objectos não implica desenha-lo de novo, mas simplesmente
alterar os valores que o definem, para isso servirá a próxima função a ser
descrita (ActualizaRobo).
5.3.4.7 ActualizaRobo.m
Este script é
responsável pela função:
ActualizaRobo( GP )
Esta função tem simplesmente como parâmetro de entrada uma
estrutura do tipo “Gestão do Plot”. Esta estrutura contém uma sub-estrutura com
os valores actualizados das posições e orientações de cada um dos componentes.
Além disso, contêm também a sub-estrutura que foi devolvida pela função DesenharRoboPZ e que indica a etiqueta
referente a cada um dos objectos do plot.
O que é então executado nesta função é um ciclo de actualização de cada um dos
valores dos objectos existentes no plot,
já que para isso só precisamos dos valores actualizados e das etiquetas de cada
objecto que se pretende actualizar.
5.3.4.8 PlotJuntas.m
A função descrita por este ficheiro é:
PlotJuntas( DM, PM, axes_PM )
Esta função desenha a trajectória de quatro juntas. A
trajectória é de 5ª ordem e é a mesma calculada pelas slaves. Como parâmetros de entrada têm-se uma estrutura do tipo
“Definição do Movimento” e que contêm toda a informação sobre todas as fases e
todos os movimentos de todas as juntas, têm-se também uma estrutura do tipo
“Plot do Movimento” onde estão incluídas o intervalo de fases a representar e
as 4 juntas que devem ser apresentadas. O último parâmetro de entrada é o handler para o axis onde vai ser efectuado o plot.
5.3.4.9 RobCOG.m
Define a função:
def = RobCOG( A,DM,COG_0, def )
Define o centro de gravidade da estrutura em determinada
fase do movimento. Para isso como parâmetros de entrada são passados a matriz
de transformação calculada pela função de cinemática directa, a estrutura
“Definição do Movimento”, o centro de gravidade inicial (com o robô humanóide
na vertical) e uma estrutura do tipo “definições”. Esta última estrutura também
é o parâmetro de saída e a razão para ela ser um parâmetro de entrada deve-se
unicamente à necessidade de ter nesta estrutura valores devolvidos por
diferentes funções e a ideia subjacente é que cada função só altere os campos
que lhe compete e deixe tudo o resto incólume.
5.3.4.10 Sim_Walking.m
No script “Sim_Walking”
está a função de locomoção implementada:
DM = Sim_Walking(DM, walk)
Os parâmetros que definem a locomoção são fornecidos através
da estrutura walk e a estrutura DM contêm além, da posição actual do
humanóide, as dimensões que alimentam as cinemáticas para o cálculo do
movimento. Como saída esta função devolve uma estrutura do tipo DM com todo o movimento descrito.
5.3.4.11 Sim_Rotate.m
Este script define
o movimento de rotação através da função:
DM = Sim_Rotate(DM, rotate)
À semelhança do que acontece com a função Sim_Walking, para esta função o
parâmetro de entrada DM contêm as
dimensões do humanóide para efectuar os cálculos do movimento. A estrutura rotate fornece as definições específicas
deste movimento, sendo essas definições as especificadas no painel referente à
rotação. Como saída é devolvida uma estrutura do tipo DM com a descrição do movimento.
5.3.4.12 Sim_Kick.m
O script “Sim_Kick”
contêm a função para a criação do movimento do pontapé:
DM = Sim_Kick(DM, kick)
E, mais uma vez, à semelhança das funções anteriores, os
parâmetros de entrada são a estrutura DM
com as dimensões do humanóide e uma estrutura kick com a definição dos parâmetros deste movimento. Como saída
têm-se a estrutura do tipo DM com a
definição do movimento.
5.3.4.13 simulate.m
O script “simulate”
permite visualizar todas as fases de movimento desenvolvidas com as
trajectórias calculadas, mostrando como será o movimento real do robô
humanóide. A função é:
simulate(DM, GP)
Não há parâmetros de saída. Os parâmetros de entrada são a
estrutura DM com os dados de cada uma
das fases do movimento criadas e a estrutura GP com as referências dos objectos que estão representados no axis.
5.3.4.14 ZeroLocalCOG.m
Este script contém
a função:
COG_XYZi = ZeroLocalCOG( DM )
Esta função devolve a posição do CoG de cada um dos
componentes do robô humanóide. Estes CoG podem depois ser usados pela função RobCOG, para o cálculo do CoG em cada
instante do movimento.
5.3.4.15 adapt.m
Esta é uma função de grande utilidade quando se trata de
aplicar movimentos simulados ao robô real ou transformar posições lidas do robô
real em posições simuladas. O que é executado no interior desta função é uma
adaptação de posições associadas à estrutura virtual em posições aplicáveis à
estrutura real.
A função é:
pos_final=adapt(scuid,position,Nrel,tipo)
Ao fornecer a esta função o identificador da slave com a qual se pretende actuar, scuid, o vector com as posições simuladas
para os 3 servos, position, o vector
com as relações de transmissão dessas juntas, Nrel, e o tipo de operação que se pretende efectuar, tipo (1-posição a enviar, 2-posição
lida). O valor devolvido é o vector de posição convertido no formato pretendido.
A Tabela 5‑5 -
Parâmetros de entrada da função adapt contém a descrição dos parâmetros de entrada da
função adapt e dos valores usados por
omissão pela função.
|
Parâmetro
|
Descrição
|
Valor por
defeito
|
|
Scuid
|
Identificador da slave
onde se vai actuar
|
-
|
|
position
|
Posição a enviar/recebida
|
-
|
|
Nrel
|
Relação de transmissão das juntas
|
[1, 1, 1]
|
|
Tipo
|
1 –
posição a enviar
|
1
|
|
-1
– posição lida
|
Tabela 5‑5 - Parâmetros de
entrada da função adapt
Esta função adapt
usa uma matriz com os offsets físicos
do humanóide e, esta matriz é auto calibravel, para isso basta invocar a função
só com um parâmetro de entrada, correspondente ao handler da comunicação RS-232.
Esta matriz é guardada automaticamente no ficheiro “matriz_calib.mat”
localizado numa pasta definida no interior da função.
|
Ficheiro
|
Função
|
Descrição
|
|
ActualizaRobo.m
|
ActualizaRobo( GP )
|
Refaz o plot actual do robô
|
|
adapt.m
|
pos_final=adapt(scuid,position,Nrel,servo)
|
Converte posições simuladas em reais e vice-versa
|
|
BuildJointMotion.m
|
|
Constrói o movimento nas juntas para o algoritmo de
locomoção
|
|
CinDir20dof.m
|
A = CinDir20dof( DM )
|
Calcula as matrizes de transformação da cinemática
directa
|
|
CinInv2R.m
|
[ang1,ang2] = CinInv2R( Pf,L,Signum )
|
Calcula a cinemática inversa 2R
|
|
CinInvHip_Liv.m
|
Q = CinInvHip_Liv( P,L )
|
Calcula a cinemática inversa para o pé livre no
algoritmo de locomoção
|
|
CinInvHip_Sup.m
|
Q = CinInvHip_Sup( P,L )
|
Calcula a cinemática inversa para o pé de suporte no
algoritmo de locomoção
|
|
CoordJuntas
|
handles = CoordJuntas( Ai,DM,handles )
|
Retorna as posições cartesianas das juntas e
restantes componentes do humanóide
|
|
data_struct.m
|
robo = data_struct()
|
Define uma estrutura com as variáveis do robô
|
|
DefineRob
|
handles = DefineRob()
|
Devolve os parâmetros estruturais do robô
(comprimentos, massas)
|
|
DesenharRoboPZ.m
|
handles = DesenharRoboPZ( GP, axis_h )
|
Faz o plot inicial do robô humanóide
|
|
GeradorTraj.m
|
[pos,vel,ace] = GeradorTraj(t,pos,vel,ace)
|
Constrói uma trajectória de 5ª
|
|
MovsList.mat
|
|
Ficheiro com os movimentos guardados
|
|
PlaneamentoJuntas.m
|
[Q,dQ,ddQ] = PlaneamentoJuntas( t,qi,qf, VEL, ACE )
|
Faz o planeamento de uma trajectória nas juntas
|
|
PlotCCarts.m
|
PlotCCarts( t,P_x,P_y,P_z )
|
Faz o plot da variação das coordenadas cartesianas
durante o movimento
|
|
PlotCOG.m
|
PlotCOG( t,COG )
|
Faz o plot da variação do CoG e CoP durante o
movimento
|
|
PlotJuntas.m
|
PlotJuntas( DM, PM, axes_PM )
|
Faz o plot da variação da posição angular das juntas
durante o movimento
|
|
Polyfit2.m
|
[COEF,dCOEF,ddCOEF] = Polyfit2( x,p,v,a )
|
Permite construir um polinómio definindo posição,
velocidade e aceleração inicias e finais
|
|
RobCOG.m
|
def = RobCOG( A,DM,COG_0, def )
|
Determina o CoG e CoP para uma dada posição do
humanóide
|
|
Rot_XX.m
|
T = Rot_XX(q)
|
Matriz de transformação com rotação em torno do eixo
xx
|
|
Rot_YY.m
|
T = Rot_YY(q)
|
Matriz de transformação com rotação em torno do eixo
yy
|
|
Rot_ZZ.m
|
T = Rot_ZZ(q)
|
Matriz de transformação com rotação em torno do eixo
zz
|
|
Sim_Kick.m
|
DM = Sim_Kick(DM, kick)
|
Devolve um movimento de um pontapé
|
|
Sim_Rotate.m
|
DM = Sim_Rotate(DM, rotate)
|
Devolve um movimento de rotação
|
|
Sim_Walking.m
|
DM = Sim_Walking(DM, walk)
|
Devolve um movimento de locomoção
|
|
Simulate.m
|
simulate(DM, GP)
|
Faz a simulação do movimento
|
|
Stairs.m
|
S = stairs(GP)
|
Devolve um objecto escadas
|
|
Tra_XX.m
|
T = Tra_XX(L)
|
Matriz de transformação com translação no eixo dos
xx
|
|
Tra_YY.m
|
T = Tra_YY(L)
|
Matriz de transformação com translação no eixo dos
yy
|
|
Tra_ZZ.m
|
T = Tra_ZZ(L)
|
Matriz de transformação com translação no eixo dos
zz
|
|
ZeroLocalCOG.m
|
COG_XYZi = ZeroLocalCOG( DM )
|
Devolve a posição cartesiana do CoG de cada
componente individualmente
|
Tabela 5‑6 - Ficheiros do TwoLegs_22dof
O GUI GestMovs é o responsável por gerir todos os movimentos
guardados. Esta janela bloqueante chamada a partir do botão GestMovs do
TwoLegs_22dof permite guardar o movimento que está a ser criado ou abrir
movimentos guardados previamente. Este GUI fornece além das possibilidades de
abrir, guardar ou criar novo movimento, a possibilidade de pré-visualizar o
movimento seleccionado.
O ficheiro MovsList.mat, armazena todos os movimentos
guardados.
Ilustração 5‑16 - Gestor de Movimentos
Um dos grandes problemas do TwoLegs_22dof deve-se ao facto
das funções de callback não serem
bloqueantes, isto é, pode haver várias funções a ser executadas ao mesmo tempo
e, como já tinha sido falado, só a última a guardar a estrutura handles é que vai ser bem sucedida,
todas as outras vão ter o seu trabalho perdido. Isto é motivo para muitas
surpresas quando se está a trabalhar com o GUI, por exemplo se se alterar o
valor de um slide das juntas e logo
de seguida mover outro slide, o
primeiro, vai voltar à posição que tinha antes de ser alterado. A solução para
estes problemas passa por garantir que enquanto uma função está a ser
processada toda a actividade visual bloqueia, para não haver hipótese de entrar
em competição outra função.
Um dos bugs incompreensível encontra-se na activação dos
menus de contexto, assim, o menu de contexto que existe associado a cada painel
nem sempre aparece. E isto, é um problema persistente durante a execução do
GUI, nem com a reinicialização da aplicação este problema fica resolvido. Isto
acontece principalmente com os painéis dos pés. Não há qualquer tipo de
explicação para este fenómeno.
No mesmo caminho dos bugs incompreensíveis encontra-se a
activação das ligações RS-232, estas ligações são efectuadas por um callback associado à textBox Ligar, mas nem sempre esse callback é chamado com o click do rato.
Este problema costuma ficar resolvido com a introdução no inicio da função de callback em questão do comando “keyboard” e, com a reinicialização do
GUI. Depois de se conseguir ligar a primeira vez com sucesso, este bug não
costuma ocorrer mais, durante a mesma sessão.
Um problema que ocorre preferencialmente quando se usa o GUI
é a falha nas comunicações já depois de estarem iniciadas. Este problema deve
estar associado ao uso de um conversor RS-232/USB, pelo menos, esta é a única
explicação plausível. Para a correção deste problema aconselha-se desligar
todas as comunicações fisicamente e voltar a tentar.
Estão assim descritos os bugs detectados, pensa-se que os
mais incompreensíveis se devam ao próprio Matlab usado e espera-se que não
existam muitos mais problemas.
A continuação do estudo do controlador PID serviu para
inferir sobre alguns pormenores relacionados com a sua influência no
comportamento global da estrutura. Para o estudo deste controlador ficou criada
uma interface gráfica de ajuda no ajuste dos parâmetros PID para um servo. Esta
interface poderá ser facilmente adaptada a vários servos e, se possível,
incluída no simulador TwoLegs_22dof para uma adaptação dinâmica dos parâmetros
do controlador local.
O controlador baseado nos sensores de força passou a incluir
a capacidade de controlo da altura da anca. Com esta nova característica foi
dado um novo passo no sentido de criar movimentos gerados apenas por estímulos
sensoriais.
Foi implementado na anca um controlador, baseado num
inclinómetro, que possibilita manter a sua postura estabilizada. Este
controlador apenas foi implementado para compensar o pitch, revelando para esse caso uma resposta satisfatória na
estabilidade da postura da anca, segundo essa direcção.
Os controladores sensoriais são ferramentas valiosas para se
avançar com movimentos que se adaptem às condições envolventes.
Os algoritmos de padrões de locomoção alcançaram este ano um
estado de desenvolvimento passível de ser directamente aplicado ao robô
humanóide. Introduziu-se na lista de padrões de locomoção o movimento de
rotação sobre si próprio, ultrapassando assim as dificuldades que o robô
humanóide cria à geração deste movimento.
A aplicação TwoLegs_22dof pode ser só o início de uma
ferramenta capaz de operar de forma eficiente o humanóide. O seu uso permite um
estudo mais aprofundado dos padrões de locomoção, criando condições para
adaptar os movimentos ao humanóide em real-time.
Esta aplicação apresenta problemas de desempenho inerentes à
plataforma em que foi criada, é talvez de pensar num futuro migrar esta
aplicação para um ambiente mais robusto e que permita integrar noções de
dinâmica, para uma análise mais rigorosa do comportamento simulado.
[1]
RUAS, Milton; Desenvolvimento
de Algoritmos de Controlo para Locomoção de um Robot Humanóide – Relatório
Final de Projecto; Julho de 2006.
[2] SILVA,
Filipe; Sistema de Manipulação e
Locomoção – Mestrado em Engenharia Mecânica; 2002-2003.
[3]
GOMES, Luís; SILVA, Mauro; Percepção e Desenvolvimento
de Unidades de Percepção e Controlo para um Robot Humanóide – Relatório Final
de Projecto; 2004/05.
[4] BEÇA,
Nuno; CARDOSO, Ângelo; Desenvolvimento e
Integração das Sub-estruturas Inferior e Superior para a Locomoção de uma
Plataforma Humanóide – Relatório Final de Projecto; 2004/05.
[5] SCIAVICCO,
Lorenzo; SICILIANO, Bruno; Modeling and
Control of Robot Manipulators; MacGraw-Hill; New York, 1996.
Ilustração
1‑1 – Robô Humanóide da Universidade de Aveiro. 6
Ilustração
2‑1 - Servomotor HITEC HS-805BB.. 19
Ilustração
2‑2 - Polias de transmissão existentes ao longo da estrutura. 20
Ilustração
2‑3 - GUI para teste do controlador PID.. 21
Ilustração
2‑4 - Movimento de flexão de uma perna. 22
Ilustração
2‑5 – Junta do tornozelo com ki=20 kp=20 kd=5. 23
Ilustração
2‑6 Junta do joelho com ki=20 kp=20 kd=0. 23
Ilustração
2‑7 – Junta da anca em malha aberta. 24
Ilustração
2‑8 – Junta do tornozelo com ki=20 kp=20 kd=5. 25
Ilustração
2‑9 – Junta do joelho com ki=20 kp=20 kd=0. 25
Ilustração
2‑10 – Junta da anca com ki=30 kp=15 kd=0. 26
Ilustração
3‑1 – Placa de acrílico com um extensómetro colado. 29
Ilustração
3‑2 – Distribuição dos sensores de força e o referencial usado. 30
Ilustração
3‑3 – Diagrama representativo de uma perna sob a vista lateral 32
Ilustração
3‑4 – Diagrama representativo de uma perna sob a vista frontal 32
Ilustração
3‑5 - Trajectória do CoP. 34
Ilustração
3‑6 - Eixo dos xx. 34
Ilustração
3‑7 - Eixo dos yy. 34
Ilustração
3‑8 - Eixo dos zz. 34
Ilustração
3‑9 - Trajectória do CoP. 35
Ilustração
3‑10 - Eixo dos xx. 35
Ilustração
3‑11 - Eixo dos yy. 35
Ilustração
3‑12 - Eixo dos zz. 35
Ilustração
3‑13 - Trajectória do CoP. 35
Ilustração
3‑14 - Eixo dos xx. 35
Ilustração
3‑15 - Eixo dos yy. 36
Ilustração
3‑16 - Eixo dos zz. 36
Ilustração
3‑17 - Modo de funcionamento do acelerómetro. 37
Ilustração
3‑18 - Acelerómetro ADXL202E. 37
Ilustração
3‑19 - Eixos de inclinação. 38
Ilustração
3‑20 – Juntas que influenciam a inclinação da anca. 39
Ilustração
3‑21 – Curva de resposta do controlador segundo o pitch. 40
Ilustração
3‑22- Movimento no teste ao controlador dos inclinómetros 41
Ilustração
3‑23 - Teste inclinómetros t=2s k=0.3. 42
Ilustração
3‑24 - Teste inclinómetros t=2s k=0.4. 43
Ilustração
3‑25 - Teste inclinómetros t=2s k=0.5. 43
Ilustração
3‑26 - Teste inclinómetros t=4s k=0.1. 44
Ilustração
3‑27 - Teste inclinómetros t=4s k=0.2. 44
Ilustração
3‑28 - Teste inclinómetros t=4s k=0.3. 45
Ilustração
3‑29 - Teste inclinómetros t=4s k=0.4. 45
Ilustração
3‑30 - Teste inclinómetros t=4s k=0.5. 46
Ilustração
3‑31 - Teste inclinómetros t=5s k=0.3. 46
Ilustração
3‑32 - Teste inclinómetros t=5s k=0.5. 47
Ilustração
4‑1 - Planos corporais e eixos de referência. 50
Ilustração
4‑2 - Centro de Gravidade (CoG) 50
Ilustração
4‑3 – Exemplo da redundância da cinemática inversa. 52
Ilustração
4‑4 - Sequência do movimento de locomoção. 55
Ilustração
4‑5 - Algoritmo para a realização de vários passos. 57
Ilustração
4‑6 - Fases do movimento de rotação. 58
Ilustração
4‑7 – Fase 1. 59
Ilustração
4‑8 – Fase 2. 59
Ilustração
4‑9 – Fase 3. 60
Ilustração
4‑10 – Fase 5. 60
Ilustração
4‑11 – Problema da rotação. 60
Ilustração
4‑12 – Fase 6. 60
Ilustração
4‑13 - Desalinhamento das juntas para o movimento lateral da anca. 61
Ilustração
4‑14 - Sequência do movimento Pontapé. 62
Ilustração
4‑15 – Fase 3. 63
Ilustração
4‑16 – Fase 4. 63
Ilustração
5‑1 - GUIDE. 65
Ilustração
5‑2 - Workspace GUIDE. 65
Ilustração
5‑3 - Criação de Menus. 66
Ilustração
5‑4 - Centros de Massa com o referencial utilizado. 71
Ilustração
5‑5 - Número de cada junta no simulador 72
Ilustração
5‑6 - Divisão do GUI 73
Ilustração
5‑7 - Aspecto visual do painel inicio. 74
Ilustração
5‑8 - Aspecto visual do painel Definição de Movimentos. 75
Ilustração
5‑9 - Menu de contexto para as juntas. 76
Ilustração
5‑10 - Aspecto visual do painel Plots do Movimentos. 77
Ilustração
5‑11 - Aspecto visual do painel Humanóide. 77
Ilustração
5‑12 – Conjunto de painéis de Movimentos Predefinidos: 78
Ilustração
5‑13 - Gestão do Plot 79
Ilustração
5‑14 - Inicialização do GUI 84
Ilustração
5‑15 - Organograma ilustrativo da estrutura robo. 87
Ilustração
5‑16 - Gestor de Movimentos. 95
Tabela
2‑1 - Valores possíveis do parâmetro param da função readjoint 14
Tabela
2‑2 - Valores do vector status retornado pela função readjoint 14
Tabela
2‑3 - Valores possíveis do parâmetro param na função applyjoint 15
Tabela
2‑4 - Valores possíveis do parâmetro param na função applycontrol 16
Tabela
2‑5 - Tipo de controladores de primeiro nível 16
Tabela
2‑6 - Tipo de parâmetro para aplicaConf 18
Tabela
2‑7 - Tipo de parâmetro a ler em lerParam.. 18
Tabela
3‑1 - Expressões da matriz jacobiano. 32
Tabela
5‑1 - Dimensões dos Elos. 69
Tabela
5‑2 - Massa dos Componentes. 69
Tabela
5‑3 - Centros de Massa dos Componentes. 70
Tabela
5‑4 - Relação de transmissão das juntas. 71
Tabela
5‑5 - Parâmetros de entrada da função adapt 92
Tabela
5‑6 - Ficheiros do TwoLegs_22dof 94
![]() ·
2 em cada pé (2x2);
·
2 em cada pé (2x2);![]() ·
1 em cada joelho (1x2);
·
1 em cada joelho (1x2);![]() ·
3 em cada anca (3x2);
·
3 em cada anca (3x2);![]() ·
2 no tronco (2x1);
·
2 no tronco (2x1);![]() ·
3 em cada braço (3x2);
·
3 em cada braço (3x2);![]() ·
2 no suporte da câmara (cabeça) (2x1).
·
2 no suporte da câmara (cabeça) (2x1).
![]() Sensores
de posição - Os sensores de posição
são potenciómetros que indicam a posição angular actual do servomotor. Há um
sensor de posição por cada servomotor.
Sensores
de posição - Os sensores de posição
são potenciómetros que indicam a posição angular actual do servomotor. Há um
sensor de posição por cada servomotor.![]() Sensores
de força - Os sensores de força
estão localizados em pequenas placas distribuídas pelos quatro cantos de cada
pé. Estes sensores servem para medir em cada instante o ponto do centro de
pressão (CoP) nesse pé.
Sensores
de força - Os sensores de força
estão localizados em pequenas placas distribuídas pelos quatro cantos de cada
pé. Estes sensores servem para medir em cada instante o ponto do centro de
pressão (CoP) nesse pé.![]() Sensores
de inclinação - Os inclinómetros ou
sensores de inclinação situam-se na zona da anca e servem para indicar a
inclinação da anca em relação ao plano da terra
Sensores
de inclinação - Os inclinómetros ou
sensores de inclinação situam-se na zona da anca e servem para indicar a
inclinação da anca em relação ao plano da terra![]() Giroscópios - Os giroscópios ainda não
têm uma aplicação específica. Estes sensores medem a velocidade angular
Giroscópios - Os giroscópios ainda não
têm uma aplicação específica. Estes sensores medem a velocidade angular![]() Câmara
CCD - A câmara CCD é os
olhos do humanóide
Câmara
CCD - A câmara CCD é os
olhos do humanóide![]() Unidade
Central
Unidade
Central![]() Master
Control Unit (MCU)
Master
Control Unit (MCU)![]() Slave Control Unit (SCU)
Slave Control Unit (SCU)![]() Continuar
o estudo do controlador local PID.
Continuar
o estudo do controlador local PID.![]() Continuar
o estudo dos sensores de força e encontrar situações de uso real durante as
movimentações do robô humanóide;
Continuar
o estudo dos sensores de força e encontrar situações de uso real durante as
movimentações do robô humanóide;![]() Iniciar
o estudo dos sensores de inclinação, implementar algoritmos de controlo
baseados na informação por eles fornecida;
Iniciar
o estudo dos sensores de inclinação, implementar algoritmos de controlo
baseados na informação por eles fornecida;![]() Estudar
e implementar padrões de locomoção aplicáveis na prática a este robô humanóide;
Estudar
e implementar padrões de locomoção aplicáveis na prática a este robô humanóide;![]() Criar
uma interface visual que permita uma interacção user-friendly com o robô.
Criar
uma interface visual que permita uma interacção user-friendly com o robô.![]() Leitura
de sensores
Leitura
de sensores![]() Leitura
de parâmetros dos servos:
Leitura
de parâmetros dos servos:![]() Parâmetros
de actuação
Parâmetros
de actuação![]() Tipo
de controlador de primeiro nível;
Tipo
de controlador de primeiro nível;![]() Parâmetros
de controlo;
Parâmetros
de controlo;![]() As
funções initcom e killcom servem exclusivamente para abrir
e fechar, respectivamente, a porta série que é utilizada pela unidade
principal.
As
funções initcom e killcom servem exclusivamente para abrir
e fechar, respectivamente, a porta série que é utilizada pela unidade
principal.![]() A
função testcom faz um pedido ao master de envio de uma sequência predefinida,
aguarda a sua recepção e verifica se houve erros na transmissão. No caso de não
haver erros o retorno desta função é zero.
A
função testcom faz um pedido ao master de envio de uma sequência predefinida,
aguarda a sua recepção e verifica se houve erros na transmissão. No caso de não
haver erros o retorno desta função é zero.![]() A
função readcanstat permite a verificação das comunicações CAN
A
função readcanstat permite a verificação das comunicações CAN![]() Para
a leitura da informação actualmente existente na SCU, há duas funções, readjoint e readspecial. A primeira permite a leitura de parâmetros associados
ao servomotor, como a posição ou a corrente consumida actual, Tabela
2‑1. A segunda função permite a leitura dos sensores
especiais que estão acoplados ao circuito de piggy-back, como por exemplo os sensores de força ou de inclinação.
Para
a leitura da informação actualmente existente na SCU, há duas funções, readjoint e readspecial. A primeira permite a leitura de parâmetros associados
ao servomotor, como a posição ou a corrente consumida actual, Tabela
2‑1. A segunda função permite a leitura dos sensores
especiais que estão acoplados ao circuito de piggy-back, como por exemplo os sensores de força ou de inclinação.![]() Como
funções de actuação são disponibilizados dois tipos de comandos, o applyjoint que permite o envio de
posições, velocidade ou simplesmente de activação do PWM nos servomotores e, o applycontrol que permite designar o tipo
de controlador activo e os parâmetros que definem esse controlador.
Como
funções de actuação são disponibilizados dois tipos de comandos, o applyjoint que permite o envio de
posições, velocidade ou simplesmente de activação do PWM nos servomotores e, o applycontrol que permite designar o tipo
de controlador activo e os parâmetros que definem esse controlador.![]() Para
activar e desactivar o PWM de várias SCU:
Para
activar e desactivar o PWM de várias SCU:![]() Para
definir a mesma velocidade para os servos de diferentes SCU
Para
definir a mesma velocidade para os servos de diferentes SCU![]() Para
aplicar valores de um tipo especifico a todos os servos de todas as slaves
Para
aplicar valores de um tipo especifico a todos os servos de todas as slaves![]() Para
ler um parâmetro em todas as slaves
Para
ler um parâmetro em todas as slaves


![]() Controlo
electrónico existente nos servos, designado por controlo em malha aberta, pois
este controlador não é acessível pelas slaves.
Controlo
electrónico existente nos servos, designado por controlo em malha aberta, pois
este controlador não é acessível pelas slaves.![]() Controlador
PID (Proporcional+Integrador+Derivativo), com os seus parâmetros directamente
acessíveis pela Unidade Principal.
Controlador
PID (Proporcional+Integrador+Derivativo), com os seus parâmetros directamente
acessíveis pela Unidade Principal.
![]()
![]()
![]()








![]() . O centro de pressão é definido por uma posição cartesiana
dada por:
. O centro de pressão é definido por uma posição cartesiana
dada por: ![]() , onde, as fórmulas de cálculo do seu valor segundo as suas
duas componentes são dadas pelas equações seguintes:
, onde, as fórmulas de cálculo do seu valor segundo as suas
duas componentes são dadas pelas equações seguintes: