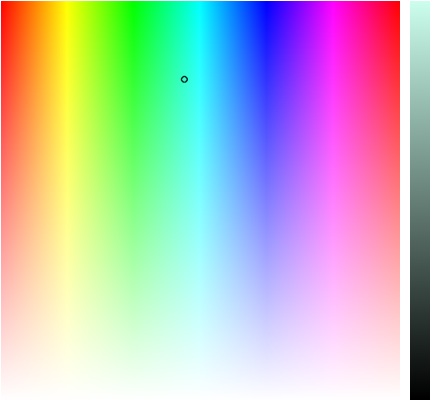
Figure 2. A H/S space with a V scale of the point marked.
The HSV model is based on the following concepts

Figure 2. A H/S space with a V scale of the point marked.
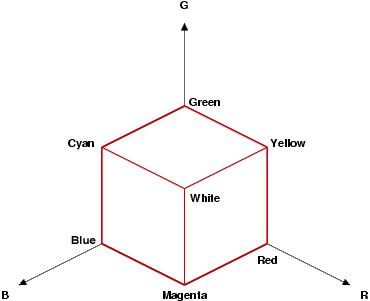
The HSV colour space has the shape of a hexagonal cone. The reasons
for this become obvious after looking at the folloiwng diagram. It
shows the standard RGB colour cube, viewed along
the black/white diagonal. This view shows the top of the HSV hexcone.
 |
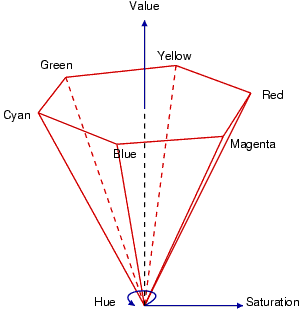 |
Figure 3. The RGB cube (left) viewed from above forming the top of the HSV hexcone (right)
| Hue | 0 to 360 degrees around the cone |
| Saturation | 0 to 1, distance from the centre of the cone |
| Value | 0 to 1, vertical position in the cone where 0 = black and 1 = white |

| #include <math.h>
void HSVtoRGB()
float mn=r,mx=r;
float delta = mx
- mn;
|