Gary B. Parker, David W. Braun, and Ingo Cyliax

Department of Computer Science, Indiana University, Bloomington, IN 47405

 It has been shown that the use of Cyclic Genetic Algorithms can be an effective means of gait generation for hexapod robot simulations. They can, with only low-level primitives, produce reasonable gaits in minimal time. In addition, their output requires little in intermediate controller complexity as it is a sequence of these primitives, which can be fed directly into the robot. In this paper, we test the applicability of these algorithms on an actual robot. A model for simulation was produced based on the measured capabilities of the Stiquito robot. This model was trained with the CGA using five random initial populations; gaits quickly evolved for all five. Tests on the actual semi-autonomous robot showed that after 1000 generations gaits comparable to the best designed by human engineers were produced.

 KEYWORDS: genetic, cyclic, robot, hexapod, gait, control

The development of learning algorithms for generating hexapod gaits is an important step in the realization of adaptive autonomous robots. This issue has been addressed resulting in viable alternatives that are usually tested on simulations, but in a few cases have also been tested on actual robots.

Marc Donner (Donner,1986) developed control strategies for the SSA six legged robot using decomposition of the task's elements and locality of control. He also developed a programming language, OWL, to provide real-time performance. Rodney Brooks (Brooks,1989) used subsumption architecture in the development of his robots. Randall Beer and John Gallagher used genetic algorithms to develop a neural net to control a simulated cockroach (Beer,1992) and showed that it was capable of controlling an actual hexapod robot (Gallagher,1994). Although promising for robots with complex controllers that have a structure capable of using a priori knowledge of tripod gaits, these works have techniques that are inappropriate for small inexpensive robots that require a repeatable sequence of activations for control.

Graham Spencer (Spencer,1992) used genetic programming and minimal a priori knowledge to evolve programs that could produce gaits. Although the programs learned were capable of producing gaits with sustained forward movement, they did not result in the optimal tripod gait. In addition, his tests were done only on simulations and not on an actual robot. In previous work (Parker,1996) we developed Cyclic Genetic Algorithms (CGAs), which generate gaits using minimal a priori knowledge. In addition, their output can be applied directly to robots at any complexity level since it is the sequence of primitive instructions that should be continually repeated to produce a gait. Tests showed that these quickly converging algorithms could produce optimal gaits on robot simulations where all robot leg capabilities were the same.

In this paper we use the CGA to develop a usable gait for an actual semi-autonomous hexapod robot. This was accomplished by developing a model with specific information taken from an individual robot. Tests were done to see if the CGA could generate reasonable gaits from this model. The results were verified by experimentation on the robot. Success was judged by measuring the distance traveled by the robot during physical tests. The results showed that the CGA was capable of generating useful gaits that were comparable to those developed by the robotics hardware technician. The algorithm was quickly converging and produced the primitives required for direct manipulation of the robot actuators. Leg coordination, inhibition, and the proper sequence and number of activations for the specific robot were all learned. The CGA should be applicable to any robot requiring a repetition of a sequence of primitives for control; no other gait control is required.

The robot used was the Stiquito II (Mills,1994). It is a small, inexpensive hexapod robot that has many of the motion characteristics of larger complex robots. Control is transmitted through a thin cable connected to the parallel port of an IBM compatible computer or through an infrared transmitter connected to a Sparc workstation. This modified version, used for the research in this paper, has autonomous characteristics that allow full freedom of movement.

The Stiquito II is made up of a plastic body, steel wire legs, nitinol wire actuators, power contacts (for the semi-autonomous version), and a control system. The nitinol actuators react by contracting when voltage is applied; this bends the wire legs. There are two actuators per leg; one to lift the leg, one to pull it back. The activation of the 12 actuators is controlled by varying the signal passed through the control system. For example: an impulse of 001000000000 results in the lifting of the left front leg; 000001000000 results in the pulling back of the second right leg. 001001000000 would activate both at the same time. Once one of these impulses is sent, the control continues to execute until it is told to stop. Repeated sequences of impulses can be devised by a person, or evolved by a CGA, so that the robot walks forward.

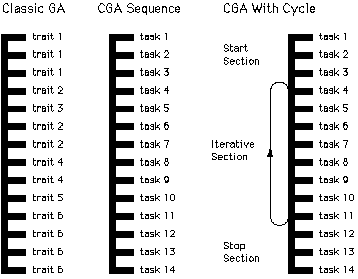
Cyclic Genetic Algorithms (CGAs) (Parker,1995) solve the problem of evolving repetitive behavior that requires continual cycles of sequential actions. They are based on Genetic Algorithms, which were introduced by John Holland (Holland,1975), and use the standard selection, crossover and mutation operators. They differ in that the CGA chromosome has a cycle of genes that can accommodate the cyclic nature of gaits. In addition, the genes can represent tasks that must be completed in a predetermined segment of time. For our purposes the tasks to be completed are a set of impulses to the robot that will result in a reasonable gait. Figure 1 shows examples of a basic GA chromosome, a CGA chromosome with tasks for its genes, and a CGA chromosome with a cycle.

CGAs can have either fixed or variable length chromosomes. Both varieties can develop cycle lengths appropriate for gait generation, but the fixed was found to be the most efficient yet adaptive enough to accommodate severe robot degradation (disablement of leg). All tests in this paper were done using a CGA with a fixed chromosome length and a population size of 64. All training sessions started with a random population.

Figure 1: GA and CGA Chromosomes

The chromosome structure used for evolution was made up of four parts (Figure 2). The coordinators affected individual legs. The back-down coordinator ensured the leg was down if moving back. The up-forward ensured that the leg was moving forward if it was up. A 12 bit number was used to represent the coordinators as there were two possible per leg. The inhibitors prevented designated pairs of legs from being moved back or forward at the same time.

A single 15 bit number represented the inhibitors. Each bit position corresponded to a specific pair of legs (15 possible). If the bit was 1 it did not allow both legs to move back at the same time even if the activation commanded it. The lower numbered leg could move while the higher numbered leg was inhibited.

The start-section was the part of the chromosome that held the activations that were executed only once. The purpose of this section was to allow the robot to transition from a standing state to a state that was part of the gait cycle. The iterative-section was repeated as many times as desired. This section was designed to form a sequence of instructions that when repeated would result in sustained cyclic behavior. The start-section was made up of a single gene and the iterative-section was made up of 12 genes.

The genes had 2 parts (Figure 2). The activations part was a 12 bit number that contained the encoding required to activate two possible primitives per leg. The nitinol that moved the leg back could either be activated or relaxed. Activated meant it was contracting and moving the leg back, relaxed meant it is being elongated by the spring action of the leg resulting in the leg moving forward. When the nitinol reached its full contraction the leg would hold its full back position. Similarly, when the nitinol was fully extended the leg would stay at its full forward position. The activation for up and relaxation for down worked in the same way. This meant the leg was always moving (unless at full throw) and each activation was either on or off.

The moves part was an 8 bit number that designated the number of times to repeat the activations part. This moves part was what gave the CGA the ability to vary the length of the sequence of primitives being sent to the robot in each cycle.

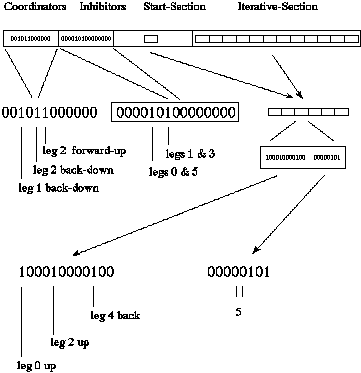
Figure 2: Cyclic Genetic Algorithm Chromosome and Gene Breakdown

The conversion from chromosome to a set of primitive commands went as follows:

1. i_act = apply inhibitors to each activation.

2. ci_act = apply coordinators to each i_act.

3. Write the ci_act from the start-section moves number of times.

4. Write a marker separating the start and iterative sections.

5. Write each ci_act from the iterative-section moves number of times.

The result was a list of primitive activations separated by a marker that could be put in a file. The robot control program ran through the list of primitives before the marker on startup sending each activation for 100 msec. The list of primitives following the marker was repeated a specified number of iterations. Again each activation was in effect for 100 msec.

3.2 GENETIC OPERATORS 

Probability for selection was determined by the individual's fitness. It was computed one activation at a time by summing the fitness of individual activations as each is applied to the current state of the simulation. The algorithm for computing an individual's fitness follows:

Fitness = 0

For each Activation do

First, the vertical activations were applied to the model (the state of the legs) which could then be used to determine which legs were on the ground. Horizontal activations were then applied to all legs but forward motion was affected only by those on the ground. The forward motion for each side was calculated by taking the average movement of the legs on that side. The activation forward motion was determined by taking the least of the two side motions. The resultant forward movement would then be reduced if the robot was out of balance or had asymmetrical movement (one side producing more thrust than the other). This was repeated from one activation to the next for each activation in the start section and continued in the iterative section until a total of 100 activations was reached. This fitness was computed for each individual in the population. Pairs of individuals were stochastically selected for reproduction.

Two types of crossover were used. Chromosome crossover was performed at two points between the genes in the iterative section resulting in section swaps between the two cycles. Gene-by-gene crossover allowed corresponding genes to swap encoded information. Crosses could happen between the individual members of the list or within the bits of the specific numbers in the list. This was done in both the start and iterative sections.

Mutation also had two operators each of which had minimal probability of occurrence. Gene-replace deleted the old gene (moves and activations) and replaced it with an entirely new one. Gene-mutate changed only one bit in the gene.

A Gene-by-gene evaluator was also used. This operator would randomly pick one or two individuals from the population and evaluate them one gene at a time. It removed genes that were significantly worse than preceding genes and reduced the moves of genes that had productive activations initially but dropped in effectiveness after some repetitions. It also moved genes with a moves number of 0 to the end so that the active genes were always at the start of the iterative section. The result of this operator was to clean up the chromosomes and speed up the elimination of poor activations.

The model was a data structure that could hold the essential information needed to determine the state of the legs and the subsequent movement calculated from the control activation input. Fields for each leg were included to store the leg's capabilities and current position. To determine each leg's resting vertical position, the robot was placed on a level surface. Legs touching the ground were at position 0, all others were relative to where their 0 position would be if they were on the ground. All future references to each leg's vertical position were relative to this initial 0 position. Each leg's horizontal position was measured relative to its at rest full forward position.

4.1 DATA STRUCTURE 

The model data structure included the following fields for each leg:

current up -- current vertical position of leg

max up -- position off ground when full up

max down -- position off ground when full down

current back -- current horizontal position of leg

max back -- position relative to full forward when full back

These fields were applicable to all legs:

rate up/down -- rate of vertical movement when actuator excited/relaxed

rate back/forward -- rate of horizontal movement when actuator excited/relaxed

Measurements to fill the position fields were taken by activating each control individually and recording the leg's maximum throw. An average rate per activation was calculated for horizontal and vertical movement by dividing the maximum throw by the minimum number of activations required to attain it.

Gaits were generated by running a CGA for 1000 generations on five starting random populations of 64 individuals. All sections of the chromosome were initialized with a random number within the appropriate range. Performance tests were done to determine the fitness of the resulting populations from each of the five starting populations. Considering the 500 and 1000 generation fitnesses, the median of each of these was selected for actual robot testing. The 500 and 1000 generation gaits were tested in sequence on the Stiquito used for the original measurements. Each run lasted for 400 activations. The robot started with its rear legs on a starting line. The distance traveled, measured in millimeters, was the shortest line from this line to the nearest leg after the run. Five runs were made for each gait.

A comparison of the performance of simulations ran on the five starting populations is shown in Figure 3. Performance at 0, 10, 100, 200, 500, and 1000 generations is shown for each. In all cases the CGA quickly improved the model’s performance and showed continual improvement over the generations.

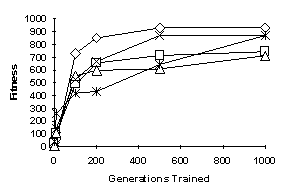
Figure 3: Comparison of the Performance of Simulations Ran on the Five Starting Populations

An analysis of the CGA 1000 generation gait revealed the following (the right legs from front to back are numbered 0, 2 & 4; the left legs from front to back are numbered 1, 3 & 5 as in Figure 4):

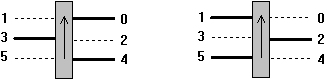
Figure 4: Stiquito Gait

1. The moves number in the start-section was 0. No initial movements were required as there were two points in the gait cycle where all legs were on or near the ground.

2. The iterative-section had five active genes. Their activations and moves resulted in the following after the inhibitors and coordinators were added:

a. Move legs (0 3 4) back and legs (1 2 5) up for five moves (shown as the first drawing in Figure 4). The solid legs are providing thrust and the dashed legs are lifting.

b. Move legs (0 3 4) back and legs () up for two moves. The first drawing is still appropriate except that the dashed legs are coming back down.

c. Move legs (0 3 4) back and legs () up for two moves. This is a duplicate of b. The activations in the original genes were different, but the application of the inhibitors and coordinators resulted in equivalent primitives.

d. Move legs (1 2 5) back and legs (0 3 4) up for five moves (shown as the second drawing in Figure 4). The solid legs are providing thrust and the dashed legs are lifting.

e. Move legs (1 2 5) back and legs () up for four moves. The second drawing is still appropriate except that the dashed legs are coming back down.

3. The result was a tripod gait with two cycles of nine activation pull backs on alternating sets of legs. There were two considerations that had to be balanced in order to get this result:

a. One of the legs had a max throw of 8.0 mm. The back-rate was 1.0, so 8 activations would result in 7.25 mm (recall that the first activation results in only 1/4 of the movement of subsequent activations). Using 9 activations would yield 8.25 mm, which would result in some leg dragging.

b. The timing of lifting and relaxing made 9 the optimal sequence length as a lift of 5 followed by a relax of 4 put the leg back to approximately its resting position due to the 1/4 movement on first activation. This timing consideration must have been sufficient to offset the drag consideration.

Tests on the actual Stiquito robot using the 500 generation and 1000 generation gaits from the median population are shown in Figure 5.

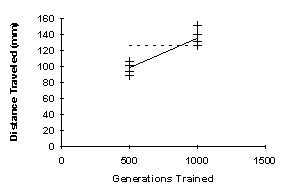
Figure 5: Tests Using the 500 and 1000 Generation Gaits on the Stiquito Robot

The horizontal dashed line shows the average robot performance over five trials using the human generated gait. The solid line connects the averages for the CGA generated gaits. As can be observed, the 1000 generation gait was, on average, roughly equivalent in performance to the gait produced by the human. This was robotics hardware technician's gait design. Using knowledge of the tripod gait, the technician determined the proper coordinators and inhibitors required to produce the gait. Timing for the duration of each of the activations in the required sequence was determined by trial and error on the robot. The result was that the entire cycle's timing was roughly equivalent to 20 activations of the control program. The technician and the CGA developed similar gaits through significantly different means.

CGAs can be successfully used to generate gaits for actual hexapod robots. The gait generator quickly produced a fast gait in simulation, which also worked well on the robot. Being comparable in performance to the best human designed gaits and possessing the ability to adapt while in operation on self-sensing robots, the CGA generated gaits can help to improve autonomous hexapod robot locomotion. 

Physical agents can have large variations in capabilities, which need to be addressed in the model. One solution may be to have dynamic models that are constantly updated by on board position and rate sensors. Our model's current construction could accommodate this change but the expense to install the required sensors would probably not make this the best option for the Stiquito. Another solution is to use a comparison of the model's performance to the actual robot's performance by making periodic cross checks. In this way, one can evolve the model with the gait or use this comparison to bias the gait's performance on the model.

The CGA converges quickly as can be observed in Figure 3, yet was shown to be adaptable in the face of extreme changes such as the loss of a leg (Parker,1995). This adaptability could be further tested by experiments on more complex robots. Hexapods with adjustable speed rates of leg movement would add another variable required for evolution. They could be trained to develop gaits optimal for the desired speed. The strength of the CGA can also be tested on our forthcoming eight-legged robots. These will not only add the complication of more legs but will also add an extra degree of freedom as the legs are more complex. In addition, adaptability tests can be more easily performed on the actual robot since leg loss can be solved while maintaining a gait with static stability. Through these tests, we can press the CGA to help define its limit in sequential cyclic control.

1) Develop gaits for other maneuvers such as turns, pivots, walk backwards, etc.

2) Use feedback in the form of leg position sensors or positional coordinates to alter the model resulting in real-time adjustments.

3) Use the CGA to generate gaits for robots that have adjustable rates of leg movement.

4) Use the CGA to generate gaits for robots that have more legs and/or degrees of freedom.

This research was supported in part by NSF Graduate Research Traineeship Grant GER93-54898.

1. Donner, M. D. (1986). Real-Time Control of Walking. Boston; Basel; Stuttgart: Birkhauser.

2. Brooks, R. A. (1989). "A Robot That Walks: Emergent Behaviors from a Carefully Evolved Network." Neural Computation (pp. 254-262).

3. Gallagher, J. C. and Beer, R. D. (1994). "Application of Evolved Locomotion Controllers to a Hexapod Robot." Technical Report CES-94-7, Department of Computer Engineering and Science, Case Western Reserve University. Refers to Beer, R. D., and Gallagher, J. C. (1992). "Evolving Dynamical Neural Networks for Adaptive Behavior." Adaptive Behavior, 1 (pp. 91-122). Cambridge: MIT Press.

4. Spencer, G. (1994). "Automatic Generation of Programs for Crawling and Walking." Advances in Genetic Programming. (pp. 335-353) K. Kinnear, Jr. (ed.), Cambridge, Ma: MIT Press.

5. Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. Ann Arbor, Mi: The University of Michigan Press.

6. Mills, J. (1994). "Stiquito II and Tensipede: Two Easy-to-Build Nitinol-Propelled Robots." Technical Report #414, Computer Science Department, Indiana University.

7. Parker, G. and Rawlins, G. (1996). "Cyclic Genetic Algorithms for the Locomotion of Hexapod Robots." Proceedings of the World Automation Congress (WAC'96), Volume 3, Robotic and Manufacturing Systems. (pp. 617-622).