Mathematical Model
:
Relaxed state
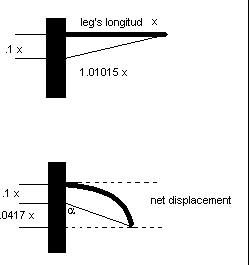
Shrunk state
This mathematical analysis is based in an ideal
function of the robot. In the above figure the X variable stands for the
leg’s length. Is important to recognize that the distance between the
body crimp connection and the leg is ten times less that of the leg.
Since we have a right triangle, applying the Pithagoras’ theorem we can
calculate the length of the relaxed Nitinol wire (X initial). That is
X initial = 1.00498756 X
The Nitinol contracts 4.8% when the temperature changes
from 30C to 80C. Knowing this, we can calculate the length of the
contracted Nitinol wire (X final) using the following formula:
(X initial – X final)/ X initial = .048
X final = .952*X initial
This will give us a new relationship:
X final = .952*1.00498756X
This will be the length of the contracted Nitinol wire.
Base on experimentation we obtain that the inclination angle (a) is approximately 87.5°.
The length of distance over passed is
OP = COS [(87.5)*(.952*1.00498756*X)]
Adding these two lengths of displacement together, the total
displacement is
(.1 + .041947)*X
remembering that X stands for the leg’s length.
The data mentioned before is exclusive for the case
when the Nitinol reaches the temperature of 80C. The question now is,
what is happening in the transition from 30C to 80C ? Based in
experimentation and using the information available in the data book, we
can expect that in one second the Nitinol reaches 80C. The temperature
increases exponentially while the pulse is applied. This behavior can be
related by the following equation:
Temp. =503.94( Exp(t/10) –1) + 27.
This equation implies that the environment temperature
is 27C. For low temperatures the Nitinol is in martensite form. This is
for temperatures between 36C up to 67.5C, this is when the Nitinol wire
is relaxed. For temperatures higher than 67.5C, the Nitinol wire changes
its form to austenite, which implies that it is contracted. Based in an
experimental graph, the percent of contraction is related in the
following equation:
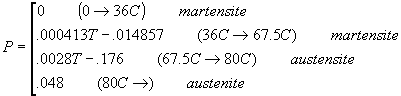
While the Nitinol contracts, the inclination angle
(a) decreases. (a) is the angle with respect to the body. This
angle varies lineally with respect to the percent of contraction, which
is related by the following equation:
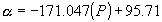
This angle will change from 87.5° up to
95.71°.
Once we have the angle of inclination we can calculate
the displacement per pulse with the equation developed before. That
is;
Displacement/pulse = .1*X +cos(a){(1 -
P)(1.00498756*X)
The ideal velocity can be determined dividing the
displacement per the time pulse period and multiplying by 60*X.
Velocity (cm/min) =displacement (60*X)/time pulse
period.
Graph Results
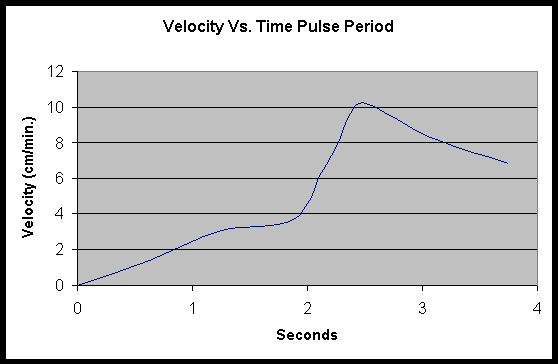
![]()